题目内容
2.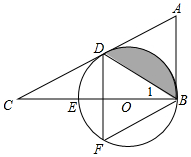 如图,在△ABC中,∠ABC=90°,D是AC边上一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D,点F在弧DEB上.
如图,在△ABC中,∠ABC=90°,D是AC边上一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D,点F在弧DEB上.(1)求证:AC是⊙O的切线.
(2)若∠A=∠F,⊙O的半径为2,求∠A的度数和阴影部分的面积.
分析 (1)连接OD,根据圆周角定理和三角形的外角的性质计算,得到∠COD+∠C=90°,根据切线的判定定理证明;
(2)根据圆周角定理得到∠BOD=2∠F,根据题意求出∠A,根据扇形面积公式计算,求出阴影部分的面积.
解答 解:(1) 连接OD,
连接OD,
∵OD=OB,
∴∠ODB=∠1,
由圆周角定理得,∠COD=∠1+∠ODB=2∠1,
∵∠C+∠A=90°,
∴∠COD+∠C=90°,
即OD⊥AC,
∴AC是⊙O的切线;
(2)由圆周角定理得,∠BOD=2∠F,
∵∠A=∠F,
∴∠BOD=2∠A,
∴∠A=60°,∠BOD=120°,
阴影部分的面积=$\frac{120π×{2}^{2}}{360}$-$\frac{1}{2}×$2×2×sin60°×2×cos60°=$\frac{4π}{3}$-$\frac{\sqrt{3}}{2}$.
点评 本题考查的是切线的判定、扇形面积的计算,掌握经过半径的外端且垂直于这条半径的直线是圆的切线、扇形的面积公式是解题的关键.

练习册系列答案
相关题目
12.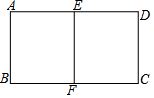 如图,在矩形ABCD中,E,F分别为,AD与BC的中点,且矩形ABCD∽矩形AEFB,$\frac{AD}{AB}$的值为( )
如图,在矩形ABCD中,E,F分别为,AD与BC的中点,且矩形ABCD∽矩形AEFB,$\frac{AD}{AB}$的值为( )
 如图,在矩形ABCD中,E,F分别为,AD与BC的中点,且矩形ABCD∽矩形AEFB,$\frac{AD}{AB}$的值为( )
如图,在矩形ABCD中,E,F分别为,AD与BC的中点,且矩形ABCD∽矩形AEFB,$\frac{AD}{AB}$的值为( )| A. | 2 | B. | $\frac{5}{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
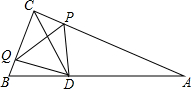 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=3cm,∠ABC的平分线交于点D,动点P,Q从点C同时出发,点P以1cm/s的速度沿射线CA方向运动,点Q以2cm/s的速度沿射线CB方向运动,当点P到达点A时,P、Q两点同时停止运动,设点P的运动时间为t(s),连接PQ,PD,QD.
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=3cm,∠ABC的平分线交于点D,动点P,Q从点C同时出发,点P以1cm/s的速度沿射线CA方向运动,点Q以2cm/s的速度沿射线CB方向运动,当点P到达点A时,P、Q两点同时停止运动,设点P的运动时间为t(s),连接PQ,PD,QD. 已知直线y=kx+b经过点A(5,0),B(1,4).
已知直线y=kx+b经过点A(5,0),B(1,4). 如图,点E是矩形ABCD的中心,△DCF为等边三角形,将△DCF沿DC翻折,F与E恰好重合,则CF:AD等于1:$\sqrt{3}$.
如图,点E是矩形ABCD的中心,△DCF为等边三角形,将△DCF沿DC翻折,F与E恰好重合,则CF:AD等于1:$\sqrt{3}$.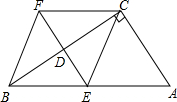 如图所示,在四边形ABFC,∠ACB=90°,BC垂直平分线EF交BC于点D,交AB于点E,且CF=AE
如图所示,在四边形ABFC,∠ACB=90°,BC垂直平分线EF交BC于点D,交AB于点E,且CF=AE