题目内容
4.已知$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{mx+ny=7}\\{nx-my=1}\end{array}\right.$的解,则$\root{3}{m+3n}$的值为( )| A. | 3 | B. | 8 | C. | 2 | D. | $\sqrt{2}$ |
分析 把x与y的值代入方程组求出m与n的值,代入原式计算即可得到结果.
解答 解:把$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$代入方程组得:$\left\{\begin{array}{l}{2m+n=7①}\\{2n-m=1②}\end{array}\right.$,
①+②×2得:5n=9,
解得:n=1.8,
把n=1.8代入②得:m=2.6,
则原式=2,
故选C
点评 此题考查了二元一次方程组的解,以及立方根,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15.已知⊙O的面积为9πcm2,若圆心O到直线的距离为3cm,则直线与⊙O的位置关系是( )
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 无 |
16.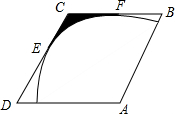 如图,菱形ABCD的边长为2,∠A=120°,以点A为圆心的圆弧与菱形ABCD的DC,BC两边相切,切点分别为点E、F,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{2}$π.
如图,菱形ABCD的边长为2,∠A=120°,以点A为圆心的圆弧与菱形ABCD的DC,BC两边相切,切点分别为点E、F,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{2}$π.
 如图,菱形ABCD的边长为2,∠A=120°,以点A为圆心的圆弧与菱形ABCD的DC,BC两边相切,切点分别为点E、F,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{2}$π.
如图,菱形ABCD的边长为2,∠A=120°,以点A为圆心的圆弧与菱形ABCD的DC,BC两边相切,切点分别为点E、F,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{2}$π.
13.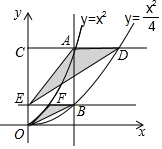 如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=$\frac{{x}^{2}}{4}$(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$的值为( )
如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=$\frac{{x}^{2}}{4}$(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$的值为( )
 如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=$\frac{{x}^{2}}{4}$(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$的值为( )
如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=$\frac{{x}^{2}}{4}$(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$的值为( )| A. | $\frac{\sqrt{2}}{6}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
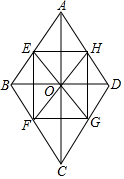 已知菱形ABCD的对角线相交于O,点E、F分别在边AB、BC上,且BE=BF,射线EO、FO分别交边CD、AD于G、H.
已知菱形ABCD的对角线相交于O,点E、F分别在边AB、BC上,且BE=BF,射线EO、FO分别交边CD、AD于G、H. 如图所示.在?ABCD中,E为BC上一点,且AD=DE,AE、DC的延长线交于点F,∠ADE=30°,求∠CEF的度数.
如图所示.在?ABCD中,E为BC上一点,且AD=DE,AE、DC的延长线交于点F,∠ADE=30°,求∠CEF的度数. 将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,求∠1+∠2的值.
将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,求∠1+∠2的值.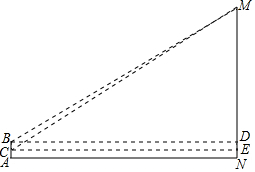 某市一湖的湖心岛有一棵百年古树,当地人称它为“乡思柳”,不乘船不易到达,每年初春时节,人们喜欢在“聚贤亭”观湖赏柳.小红和小军很想知道“聚贤亭”与“乡思柳”之间的大致距离,于是,有一天,他们俩带着侧倾器和皮尺来测量这个距离.测量方法如下:如图,首先,小军站在“聚贤亭”的A处,用侧倾器测得“乡思柳”顶端M点的仰角为23°,此时测得小军的眼睛距地面的高度AB为1.7米,然后,小军在A处蹲下,用侧倾器测得“乡思柳”顶端M点的仰角为24°,这时测得小军的眼睛距地面的高度AC为1米.请你利用以上测得的数据,计算“聚贤亭”与“乡思柳”之间的距离AN的长(结果精确到1米).(参考数据:sin23°≈0.3907,cos23°≈0.9205,tan23°≈0.4245,sin24°≈0.4067,cos24°≈0.9135,tan24°≈0.4452.)
某市一湖的湖心岛有一棵百年古树,当地人称它为“乡思柳”,不乘船不易到达,每年初春时节,人们喜欢在“聚贤亭”观湖赏柳.小红和小军很想知道“聚贤亭”与“乡思柳”之间的大致距离,于是,有一天,他们俩带着侧倾器和皮尺来测量这个距离.测量方法如下:如图,首先,小军站在“聚贤亭”的A处,用侧倾器测得“乡思柳”顶端M点的仰角为23°,此时测得小军的眼睛距地面的高度AB为1.7米,然后,小军在A处蹲下,用侧倾器测得“乡思柳”顶端M点的仰角为24°,这时测得小军的眼睛距地面的高度AC为1米.请你利用以上测得的数据,计算“聚贤亭”与“乡思柳”之间的距离AN的长(结果精确到1米).(参考数据:sin23°≈0.3907,cos23°≈0.9205,tan23°≈0.4245,sin24°≈0.4067,cos24°≈0.9135,tan24°≈0.4452.)