题目内容
5.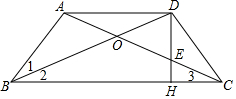 如图,已知四边形ABCD中,AC与BD相交于点O,OA=OD,∠1=∠2=∠3,∠BAC=90°,DH⊥BC于H,DH交AC于E.
如图,已知四边形ABCD中,AC与BD相交于点O,OA=OD,∠1=∠2=∠3,∠BAC=90°,DH⊥BC于H,DH交AC于E.(1)求证:AB=DC;
(2)求证:DE=$\frac{1}{2}$OC.
分析 (1)只要证明△AOB≌DOC即可.
(2)只要证明△ODE是等边三角形,△ODC是含有30度角的直角三角形即可解决问题.
解答  证明:(1)∵∠2=∠3,
证明:(1)∵∠2=∠3,
∴OB=OC,
在△AOB和△DOC中,
$\left\{\begin{array}{l}{OA=OD}\\{∠AOB=∠DOC}\\{OB=OC}\end{array}\right.$,
∴△AOB≌DOC,
∴AB=DC.
(2)∵△AOB≌△DOC,
∴∠ODC=∠BAO=90°,
∵∠1=∠2=∠3,∠1+∠2+∠3=90°,
∴∠1=∠2=∠3=30°,
∴∠AOB=60°,
∵DH⊥BC,
∴∠EHC=90°,
∴∠DEO=∠CEH=60°,
∴△DOE是等边三角形,
∴OD=OE=DE,
在Rt△ODC中,∵∠ODC=90°,∠DCO=30°,
∴OC=2OD,∵OD=OE,
∴OE=EC,
∴DE=$\frac{1}{2}$OC.
点评 本题考查全等三角形的判定和性质、等边三角形的判定和性质、直角三角形30度角的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
15.已知⊙O的半径为$\sqrt{5}$,直线l和点O的距离为d,如果直线l和⊙O有公共点,那么( )
| A. | d>$\sqrt{5}$ | B. | d=$\sqrt{5}$ | C. | 0≤d≤$\sqrt{5}$ | D. | 0<d<$\sqrt{5}$ |
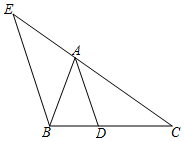 已知△ABC中,D为边BC上一点,AB=AD=CD.
已知△ABC中,D为边BC上一点,AB=AD=CD. 如图四边形ABCD中,∠C=90°,BC=1,DC=2,AB=$\sqrt{14}$,AD=3,求出这个四边形的面积.
如图四边形ABCD中,∠C=90°,BC=1,DC=2,AB=$\sqrt{14}$,AD=3,求出这个四边形的面积.