题目内容
15.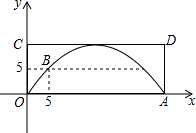 如图,一座抛物线型拱桥,桥面CD与水面平行,在正常水位时桥下水面宽OA为30米,拱桥B处为警戒水位标识,点B到OC的水平距离和它到水面OA的距离都为5米.
如图,一座抛物线型拱桥,桥面CD与水面平行,在正常水位时桥下水面宽OA为30米,拱桥B处为警戒水位标识,点B到OC的水平距离和它到水面OA的距离都为5米.(1)按如图所示的直角坐标系,求该抛物线的函数表达式;
(2)求在正常水位时桥面CD距离水面的高度;
(3)一货船载长方体货箱高出水面2米(船高不计).若要使货船在警戒水位时能安全通过该拱桥,则货箱最宽应为多少米?
分析 (1)设抛物线解析式为:y=ax2+bx,将点B(5,5)、点A(30,0)代入求得a、b的值即可得抛物线解析式;
(2)将抛物线解析式配方可得其最大值,即最大高度;
(3)使货船在警戒水位时能安全通过该拱桥则y=7,求得x的值,即可的货箱的最大宽度.
解答 解:(1)根据题意,设抛物线解析式为:y=ax2+bx,
将点B(5,5)、点A(30,0)代入,得:
$\left\{\begin{array}{l}{25a+5b=5}\\{900a+30b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{25}}\\{b=\frac{6}{5}}\end{array}\right.$.
故抛物线解析式为:y=-$\frac{1}{25}$x2+$\frac{6}{5}$x;
(2)∵y=-$\frac{1}{25}$x2+$\frac{6}{5}$x=-$\frac{1}{25}$(x-15)2+9,
∴当x=15时,y取得最大值,最大值为9,
故在正常水位时桥面CD距离水面的高度为9米;
(3)根据题意,当y=7时,有-$\frac{1}{25}$x2+$\frac{6}{5}$x=7,
解得:x1=15+5$\sqrt{2}$,x2=15-5$\sqrt{2}$,
则货箱最宽为:15+5$\sqrt{2}$-(15-5$\sqrt{2}$)=10$\sqrt{2}$米.
答:若要使货船在警戒水位时能安全通过该拱桥,则货箱最宽应为10$\sqrt{{2}_{\;}}$米.
点评 本题主要考查二次函数的实际应用,待定系数法求出抛物线解析式是解题的关键,结合题意理解不同水位对应的函数关系是解题的关键.

练习册系列答案
相关题目
 某同学在距电视塔BC塔底水平距离200米的A处,看塔顶C的仰角为20°(不考虑身高因素),则此塔BC的高约为( )
某同学在距电视塔BC塔底水平距离200米的A处,看塔顶C的仰角为20°(不考虑身高因素),则此塔BC的高约为( )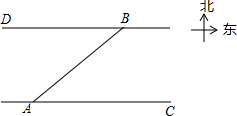 如图,一艘客轮以30km/h的速度由A码头出发沿北偏东53°方向航行至B码头,已知A、B两码头所在的河岸均为东西走向,河宽为16km,求该客轮至少用多长时间才能到达B码头?
如图,一艘客轮以30km/h的速度由A码头出发沿北偏东53°方向航行至B码头,已知A、B两码头所在的河岸均为东西走向,河宽为16km,求该客轮至少用多长时间才能到达B码头?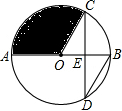 如图,AB是⊙O的直径,弦CD交AB于点E,且E是CD的中点,∠CDB=30°,CD=6$\sqrt{3}$,则阴影部分面积为( )
如图,AB是⊙O的直径,弦CD交AB于点E,且E是CD的中点,∠CDB=30°,CD=6$\sqrt{3}$,则阴影部分面积为( )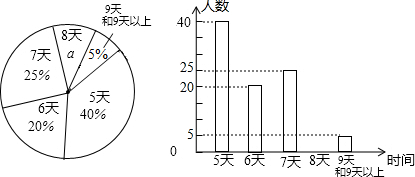
 用圆规、直尺作图,不写作法,但要保留作图痕迹.
用圆规、直尺作图,不写作法,但要保留作图痕迹. 如图,要在渠岸AB上找一点D,在点D处开沟,把水渠中的水引到C点,要使沟最短,线段CD与渠岸AB的位置关系应是垂直,理由是垂线段最短.
如图,要在渠岸AB上找一点D,在点D处开沟,把水渠中的水引到C点,要使沟最短,线段CD与渠岸AB的位置关系应是垂直,理由是垂线段最短.