题目内容
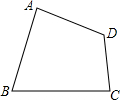 如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,且四边形ABCD的面积为49cm2,则点A到BC的距离是
如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,且四边形ABCD的面积为49cm2,则点A到BC的距离是考点:全等三角形的判定与性质
专题:
分析:如图,作辅助线;证明四边形AMCN为矩形;证明△ABM≌△ADN,得到AM=AN,四边形AMCN为正方形,即可解决问题.
解答: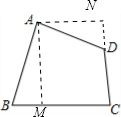 解:如图,过点A作AM⊥BC,AN⊥CD,交CD的延长线于点N;
解:如图,过点A作AM⊥BC,AN⊥CD,交CD的延长线于点N;
∵∠BAD=∠BCD=90°,
∴四边形AMCN为矩形,
∴∠MAN=90°,而∠BAD=90°,
∴∠BAM=∠DAN;
在△ABM与△ADN中,
,
∴△ABM≌△ADN(AAS),
∴AM=AN,四边形AMCN为正方形;
∵四边形ABCD的面积为49cm2,
∴AM2=49,AM=7(cm).
故答案为7cm.
 解:如图,过点A作AM⊥BC,AN⊥CD,交CD的延长线于点N;
解:如图,过点A作AM⊥BC,AN⊥CD,交CD的延长线于点N;∵∠BAD=∠BCD=90°,
∴四边形AMCN为矩形,
∴∠MAN=90°,而∠BAD=90°,
∴∠BAM=∠DAN;
在△ABM与△ADN中,
|
∴△ABM≌△ADN(AAS),
∴AM=AN,四边形AMCN为正方形;
∵四边形ABCD的面积为49cm2,
∴AM2=49,AM=7(cm).
故答案为7cm.
点评:该题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是作辅助线,构造全等三角形,灵活运用全等三角形的判定及其性质来分析、判断、推理或解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
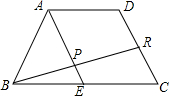 如图,B是平行四边形AECD边CE延长线上一点,且EB=EC,R为CD的中点,BR交AE于点P,则EP:AP=( )
如图,B是平行四边形AECD边CE延长线上一点,且EB=EC,R为CD的中点,BR交AE于点P,则EP:AP=( )A、
| ||
B、
| ||
C、
| ||
D、
|
 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3. 如图,一艘渔船正由西向东追赶鱼群,在A处测得小岛C在船的北偏东60°方向,距离A处80千米,此时渔船接到通知,以小岛C为中心周围30海里以内为我军导弹部队军事演习的着弹危险区,问这艘渔船继续向前追赶鱼群,是否有进入区域的可能?
如图,一艘渔船正由西向东追赶鱼群,在A处测得小岛C在船的北偏东60°方向,距离A处80千米,此时渔船接到通知,以小岛C为中心周围30海里以内为我军导弹部队军事演习的着弹危险区,问这艘渔船继续向前追赶鱼群,是否有进入区域的可能? 如图,AB是⊙O的直径,BE是弦,C是劣弧BE的中点,过C作CD⊥AB于D,CD交BE于点F,过C作CG∥BE交AB延长线于点G.
如图,AB是⊙O的直径,BE是弦,C是劣弧BE的中点,过C作CD⊥AB于D,CD交BE于点F,过C作CG∥BE交AB延长线于点G.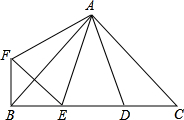 如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF、则下列结论:
如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF、则下列结论: