题目内容
如果∠A是锐角,则下列结论正确个数为( )个.
①
=sinA-1;②sinA+cosA>1;③tanA>sinA;④cosA=sin(90°-∠A)
①
| (sinA-1)2 |
| A、1 | B、2 | C、3 | D、4 |
考点:同角三角函数的关系
专题:
分析:先画出图形,根据锐角三角函数的定义求出sinA=
,cosA=
,tanA=
,再分别代入求出,即可判断正误.
| a |
| c |
| b |
| c |
| a |
| b |
解答:解:
∵在Rt△ACB中,∠C=90°,AC=b,BC=a,AB=c,如图,
sinA=
,cosA=
,tanA=
,
∴
=1-sinA,sinA+cosA=
+
=
>1,tanA>sinA,
∵cosA=
,sin(90°-∠A)=sinB=
,
∴cosA=sin(90°-∠A),
即正确的有②③④,共3个,
故选C.

∵在Rt△ACB中,∠C=90°,AC=b,BC=a,AB=c,如图,
sinA=
| a |
| c |
| b |
| c |
| a |
| b |
∴
| (sinA-1)2 |
| a |
| c |
| b |
| c |
| a+b |
| c |
∵cosA=
| b |
| c |
| b |
| c |
∴cosA=sin(90°-∠A),
即正确的有②③④,共3个,
故选C.
点评:本题考查了锐角三角函数的定义的应用,主要考查学生的计算能力和辨析能力,注意:在Rt△ACB中,∠C=90°,AC=b,BC=a,AB=c,sinA=
,cosA=
,tanA=
.
| a |
| c |
| b |
| c |
| a |
| b |

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
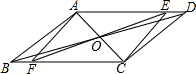 如图,在?ABCD中,对角线AC、BD交于点O,并且∠DAC=60°,∠ADB=15°.点E是AD边上一动点,延长EO交BC于点F.当点E从D点向A点移动过程中(点E与点D,A不重合),则四边形AFCE的变化是( )
如图,在?ABCD中,对角线AC、BD交于点O,并且∠DAC=60°,∠ADB=15°.点E是AD边上一动点,延长EO交BC于点F.当点E从D点向A点移动过程中(点E与点D,A不重合),则四边形AFCE的变化是( )| A、平行四边形→矩形→平行四边形→菱形→平行四边形 |
| B、平行四边形→菱形→平行四边形→矩形→平行四边形 |
| C、平行四边形→矩形→平行四边形→正方形→平行四边形 |
| D、平行四边形→矩形→菱形→正方形→平行四边形 |
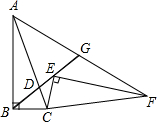 如图,在Rt△ABC中,∠B=90°,sin∠BAC=
如图,在Rt△ABC中,∠B=90°,sin∠BAC=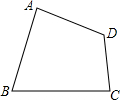 如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,且四边形ABCD的面积为49cm2,则点A到BC的距离是
如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,且四边形ABCD的面积为49cm2,则点A到BC的距离是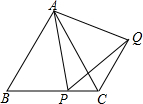 如图,已知△ABC为等边三角形,P为BC上一点,△APQ为等边三角形.
如图,已知△ABC为等边三角形,P为BC上一点,△APQ为等边三角形. 如图,“石头、剪刀、布”是民间广为流传的游戏.距报道,“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.“剪刀石头布”比赛时双方每次任意出“剪刀”、“石头”、“布”这三种手势中的一种,规则为:剪刀胜布,布胜石头,石头胜剪刀,若双方出现相同手势,则算打平.若小刚和小明两人只比赛一局,那么两人打平的概率P=
如图,“石头、剪刀、布”是民间广为流传的游戏.距报道,“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.“剪刀石头布”比赛时双方每次任意出“剪刀”、“石头”、“布”这三种手势中的一种,规则为:剪刀胜布,布胜石头,石头胜剪刀,若双方出现相同手势,则算打平.若小刚和小明两人只比赛一局,那么两人打平的概率P= 如图所示,直线AB、CD相交于点O,若∠AOC=(2x+50)°,∠BOD=(3x)°,求∠AOD的度数.
如图所示,直线AB、CD相交于点O,若∠AOC=(2x+50)°,∠BOD=(3x)°,求∠AOD的度数.