题目内容
 如图,一艘渔船正由西向东追赶鱼群,在A处测得小岛C在船的北偏东60°方向,距离A处80千米,此时渔船接到通知,以小岛C为中心周围30海里以内为我军导弹部队军事演习的着弹危险区,问这艘渔船继续向前追赶鱼群,是否有进入区域的可能?
如图,一艘渔船正由西向东追赶鱼群,在A处测得小岛C在船的北偏东60°方向,距离A处80千米,此时渔船接到通知,以小岛C为中心周围30海里以内为我军导弹部队军事演习的着弹危险区,问这艘渔船继续向前追赶鱼群,是否有进入区域的可能?考点:解直角三角形的应用-方向角问题
专题:
分析:过点C作CD⊥AB于点D,根据在A处测得小岛C在船的北偏东60°方向,距离A处80千米可知∠CAD=30°,故CD=
AC=40,再比较CD与30海里的大小即可.
| 1 |
| 2 |
解答: 解:没有进入区域的可能.
解:没有进入区域的可能.
过点C作CD⊥AB于点D,
∵在A处测得小岛C在船的北偏东60°方向,距离A处80千米•,
∴∠CAD=30°,
∴CD=
AC=40(海里),
∵40>30,
∴没有进入区域的可能.
 解:没有进入区域的可能.
解:没有进入区域的可能.过点C作CD⊥AB于点D,
∵在A处测得小岛C在船的北偏东60°方向,距离A处80千米•,
∴∠CAD=30°,
∴CD=
| 1 |
| 2 |
∵40>30,
∴没有进入区域的可能.
点评:本题考查的是解直角三角形的应用-方向角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
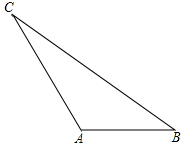 如图所示,在△ABC中,AB=1,AC=
如图所示,在△ABC中,AB=1,AC= 如图,AC和BD相交于点O,OA=OC,OB=OD.求证:CD=AB.
如图,AC和BD相交于点O,OA=OC,OB=OD.求证:CD=AB. 如图所示,在△ABC中,∠B=45°,∠C=30°,AB=4
如图所示,在△ABC中,∠B=45°,∠C=30°,AB=4 如图是由4个边长为1的正方形组成的图形,请求出∠ABC的度数.
如图是由4个边长为1的正方形组成的图形,请求出∠ABC的度数.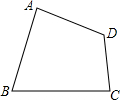 如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,且四边形ABCD的面积为49cm2,则点A到BC的距离是
如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,且四边形ABCD的面积为49cm2,则点A到BC的距离是 如图,“石头、剪刀、布”是民间广为流传的游戏.距报道,“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.“剪刀石头布”比赛时双方每次任意出“剪刀”、“石头”、“布”这三种手势中的一种,规则为:剪刀胜布,布胜石头,石头胜剪刀,若双方出现相同手势,则算打平.若小刚和小明两人只比赛一局,那么两人打平的概率P=
如图,“石头、剪刀、布”是民间广为流传的游戏.距报道,“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.“剪刀石头布”比赛时双方每次任意出“剪刀”、“石头”、“布”这三种手势中的一种,规则为:剪刀胜布,布胜石头,石头胜剪刀,若双方出现相同手势,则算打平.若小刚和小明两人只比赛一局,那么两人打平的概率P=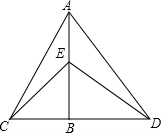 如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,下列说法中:①△ABC≌△DBE;②△ACB≌△ABD;③△CBE≌△BED;④△ACE≌△ADE.正确的是( )
如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,下列说法中:①△ABC≌△DBE;②△ACB≌△ABD;③△CBE≌△BED;④△ACE≌△ADE.正确的是( )