Question

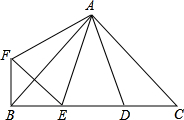如图，∠BAC=∠DAF=90°，AB=AC，AD=AF，点D、E为BC边上的两点，且∠DAE=45°，连接EF、BF、则下列结论：
①△AED≌△AEF；②BE+DC＞DE；③BE²+DC²=DE²，
其中正确的有（　　）

• A、0个
• B、1个
• C、2个
• D、3个

Answer 1

考点：全等三角形的判定与性质,勾股定理

专题：

分析：如图，证明△ABF≌△ACD，BF=CD；证明△AED≌△AEF，得到DE=EF；证明∠EBF=90°，即可解决问题．

解答：解：如图，∵∠BAC=∠DAF=90°，
∴∠BAF=∠DAC；在△ABF与△ACD中，

AB=AC ∠FAB=∠DAC AF=AD

，
∴△ABF≌△ACD（SAS），
∴∠ABE=∠C=45°，BF=CD；
∵∠EAD=45°，
∴∠BAE+∠CAD=90°-45°=45°；
∵∠BAF=∠CAD，
∴∠BAF+∠BAE=45°，
∴∠EAF=∠EAD；在△AED与△AEF中，

AE=AE ∠EAF=∠EAD AF=AD

，
∴△AED≌△AEF（SAS），
∴DE=EF；
∵BE+BF＞EF，而BF=CD，
∴BE+DC＞DE；
∵∠EBF=90°，
∴BE²+BF²=EF²，
即BE²+DC²=DE²
综上所述①②③均正确，
故选D．

点评：该题主要考查了全等三角形的判定及其性质的应用问题；解题的关键是深入观察图形，准确找出图形中隐含的等量关系，灵活运用全等三角形的判定及其性质来分析、解答．