题目内容
5. 如图,在Rt△ABC中,∠BAC=30°,AB=$\sqrt{3}$,将△ABC绕顶点C顺时针旋转至△A′B′C的位置,且A、CB′三点在同一条直线上,则点A经过的路线的长度是$\frac{4π}{3}$(结果保留π).
如图,在Rt△ABC中,∠BAC=30°,AB=$\sqrt{3}$,将△ABC绕顶点C顺时针旋转至△A′B′C的位置,且A、CB′三点在同一条直线上,则点A经过的路线的长度是$\frac{4π}{3}$(结果保留π).
分析 点A经过的路线即以C为圆心,以AC的长为半径的弧.利用解直角三角形的知识求得AC的长和∠ACB的度数,从而求得∠ACA′的度数,再根据弧长公式进行计算.
解答 解:∵将△ABC绕顶点C顺时针旋转至△A′B′C′的位置,
∴∠ACB=∠A′CB′;又∵∠ABC=90°,∠BAC=30°,
∴∠ACB=∠A′CB′=60°;
∵A、C、B'三点在同一条直线上,
∴∠ACA′=120°.
又∵∠BAC=30°,AB=$\sqrt{3}$,
∴AC=2,
∴点A经过的路线的长度=$\frac{120π×2}{180}$=$\frac{4π}{3}$.
故答案为$\frac{4π}{3}$.
点评 本题考查了弧长的计算、旋转的性质、解直角三角形的知识.求出∠ACA′的度数以及AC的长度是解题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
20.下列窗花图案中是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.下列各数,不是无理数的是( )
| A. | 0.5 | |
| B. | $\sqrt{8}$ | |
| C. | 3π | |
| D. | 0.282282228…(两个8之间依次多1个2) |
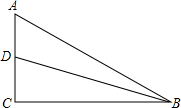 如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,交AC于D,若CD=3,AB=8,则△ABD的面积12.
如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,交AC于D,若CD=3,AB=8,则△ABD的面积12.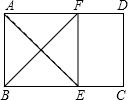 如图,在矩形ABCD中,∠A的平分线交BC于E,∠B的平分线交AD于F,求证:四边形ABEF是正方形.
如图,在矩形ABCD中,∠A的平分线交BC于E,∠B的平分线交AD于F,求证:四边形ABEF是正方形.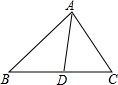 如图,△ABC,AD平分∠BAC交BC于点D,求证:$\frac{BD}{CD}$=$\frac{AB}{AC}$.
如图,△ABC,AD平分∠BAC交BC于点D,求证:$\frac{BD}{CD}$=$\frac{AB}{AC}$.