题目内容
8.如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.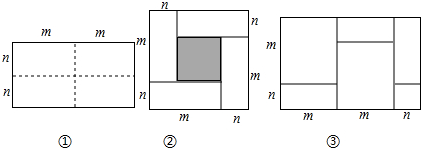
(1)按要求填空:
①你认为图②中的阴影部分的正方形的边长等于m-n;
②请用两种不同的方法表示图②中阴影部分的面积:
方法1:(m-n)2
方法2:(m+n)2-4mn
③观察图②,请写出代数式(m+n)2,(m-n)2,mn这三个代数式之间的等量关系:(m-n)2=(m+n)2-4mn;
(2)根据(1)题中的等量关系,解决如下问题:若|m+n-6|+|mn-4|=0,求(m-n)2的值.
(3)实际上有许多代数恒等式可以用图形的面积来表示,如图③,它表示了(2m+n)(m+n)=2m2+3mn+n2.
分析 (1)①观察可得阴影部分的正方形边长是m-n;
②方法1:阴影部分的面积就等于边长为m-n的小正方形的面积;方法2:边长为m+n的大正方形的面积减去4个长为m,宽为n的长方形面积;
③根据以上相同图形的面积相等可得;
(2)根据|m+n-6|+|mn-4|=0可得m+n=6、mn=4,利用(1)中结论(m-n)2=(m+n)2-4mn计算可得;
(3)根据:大长方形面积等于长乘以宽或两个边长分别为m、n的正方形加上3个长为m、宽为n的小长方形面积和列式可得.
解答 解:(1)①阴影部分的正方形边长是m-n.
②方法1:阴影部分的面积就等于边长为m-n的小正方形的面积,即(m-n)2,
方法2:边长为m+n的大正方形的面积减去4个长为m,宽为n的长方形面积,即(m+n)2-4mn;
③(m-n)2=(m+n)2-4mn.
(2))∵|m+n-6|+|mn-4|=0,
∴m+n-6=0,mn-4=0,
∴m+n=6,mn=4
∵由(1)可得(m-n)2=(m+n)2-4mn
∴(m-n)2=(m+n)2-4mn=62-4×4=20,
∴(m-n)2=20;
(3)根据大长方形面积等于长乘以宽有:(2m+n)(m+n),
或两个边长分别为m、n的正方形加上3个长为m、宽为n的小长方形面积和有:2m2+3mn+n2,
故可得:(2m+n)(m+n)=2m2+3mn+n2.
故答案为:(1)m-n;(2)①(m-n)2,②(m+n)2-4mn,③(m-n)2=(m+n)2-4mn;(3)(2m+n)(m+n)=2m2+3mn+n2.
点评 本题考查了完全平方公式的几何意义,认真观察图形以及掌握正方形、长方形的面积公式计算是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.下列方程组的解中是二元一次方程组$\left\{\begin{array}{l}{2x+y=2}\\{-x+y=5}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$ |
20.下列窗花图案中是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.下列各数,不是无理数的是( )
| A. | 0.5 | |
| B. | $\sqrt{8}$ | |
| C. | 3π | |
| D. | 0.282282228…(两个8之间依次多1个2) |
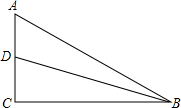 如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,交AC于D,若CD=3,AB=8,则△ABD的面积12.
如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,交AC于D,若CD=3,AB=8,则△ABD的面积12.