题目内容
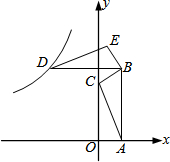 如图,在平面直角坐标系上,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,AB=3,△ABC的面积为
如图,在平面直角坐标系上,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,AB=3,△ABC的面积为| 3 |
| 2 |
(1)求点B的坐标;
(2)将△ABC以点B为旋转中心顺时针方向旋转90° 得到△DBE,一反比例函数图象恰好过点D时,求反比例函数解析式.
考点:反比例函数系数k的几何意义,待定系数法求反比例函数解析式,坐标与图形变化-旋转
专题:
分析:(1)根据三角形的面积公式即可求得OA的长,则B的坐标即可求解;
(2)首先求得D的坐标,利用待定系数法求得函数的解析式.
(2)首先求得D的坐标,利用待定系数法求得函数的解析式.
解答: 解:(1)解:AB∥y轴,
解:(1)解:AB∥y轴,
∴S△ABC=
AB•OA
=
×3×OA=
,
∴OA=1
∴B(1,3).
(2)解:AB=BD=3
∠ABD=90°
∴DB∥x轴
∴DF=3-1=2
∴D(-2,3),
设反比例解析式为y=
,
3=
,得k=-6.
∴y=-
.
 解:(1)解:AB∥y轴,
解:(1)解:AB∥y轴,∴S△ABC=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 2 |
∴OA=1
∴B(1,3).
(2)解:AB=BD=3
∠ABD=90°
∴DB∥x轴
∴DF=3-1=2
∴D(-2,3),
设反比例解析式为y=
| k |
| x |
3=
| k |
| -2 |
∴y=-
| 6 |
| x |
点评:本题考查了待定系数法求函数的解析式,正确根据三角形的面积公式求得OA的长是关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 某数学兴趣小组在探索“圆的有关相交弦问题”时,
某数学兴趣小组在探索“圆的有关相交弦问题”时,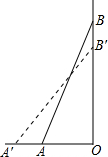 如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为3m,梯子的顶端A向外移动到A′,使梯子的底端A′到墙根O的距离等于4m,同时梯子的顶端B下降至B′,求BB′的长(梯子AB的长为5m).
如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为3m,梯子的顶端A向外移动到A′,使梯子的底端A′到墙根O的距离等于4m,同时梯子的顶端B下降至B′,求BB′的长(梯子AB的长为5m). 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.已知△ABC:
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.已知△ABC:
 如图,四边形ABCD是梯形,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,若AB=2,AD=3,则tanB的值为
如图,四边形ABCD是梯形,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,若AB=2,AD=3,则tanB的值为