题目内容
利用下面的图形分别给出勾股定理的两种证明．
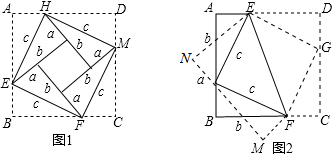
考点：勾股定理的证明
专题：
分析：直接利用正方形面积以及三角形面积公式进而得出等式即可．
解答：证明：∵四边形HEFM的面积为：c2，
四边形HEFM的面积还可以表示为：4×
ab+（b-a）2=a2+b2，
∴a2+b2=c2；
∵四边形ABCD的面积为：（a+b）2，
四边形ABCD的面积还可以表示为：4×
ab+c2=c2+2ab，
∴a2+b2=c2．
四边形HEFM的面积还可以表示为：4×
| 1 |
| 2 |
∴a2+b2=c2；
∵四边形ABCD的面积为：（a+b）2，
四边形ABCD的面积还可以表示为：4×
| 1 |
| 2 |
∴a2+b2=c2．
点评：此题主要考查了勾股定理的证明，利用图形面积关系是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
已知：关于x的一元二次方程mx2-（4m+1）x+3m+3=0 （m＞1）．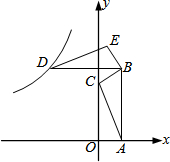
如图，在平面直角坐标系上，△ABC的顶点A和C分别在x轴、y轴的正半轴上，且AB∥y轴，AB=3，△ABC的面积为
如图，已知△ABC为等腰直角三角形，AC=BC=8，点D在BC上，CD=2，E为AB边上的动点，则△CDE周长的最小值是
如图，如果从半径为6cm的圆形纸片中剪去