题目内容
6．
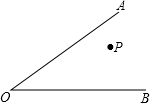如图，点P为∠AOB内一定点，小明从点P出发，先到达OA边上的某一位置M，再达到OB边上的某一位置N，最后返回点P．设计一条路线，使小明走的总路径最短，在图中确定此时点M和点N的位置（保留画图痕迹，但不写画法）．
分析 作P关于OA，OB的对称点E，F．连接EF交OA于M，交OB于N，连接PM、PN，则PM+MN+NP的值最小．
解答 解：作P关于OA，OB的对称点E，F．连接EF交OA于M，交OB于N，连接PM、PN，则PM+MN+NP的值最小．
理由：∵PM+MN+PN=EM+MN+NF=EF，
∴根据两点之间线段最短，可知PM+MN+PN的值最小．
点评 本题考查的是轴对称--最短路线问题，根据轴对称确定最短路线是解题的关键，注意等边三角形的性质的灵活运用．
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
如图，在四边形ABCD中，AB=20，BC=15，CD=7，AD=24，∠B=90°．
14．若（x-3）（x2+ax+b）的积中不含x的二次项和一次项，则a和b的值（ ）
| A． | a=0；b=2 | B． | a=3；b=9 | C． | a=-1；b=2 | D． | a=2；b=4 |
如图，已知∠ACD是△ABC的一个外角，∠ACD=130°，∠B=70°，则∠A的度数为60°．
如图，一根木棍斜靠在与地面（OM）垂直的墙（ON）上，设木棍中点为P，若木棍A端沿墙下滑，且B沿地面向右滑行．在此滑动过程中，点P到点O的距离（ ）
18．下列图形是四种运动品牌的商标，其中是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
15．△ABC与△DEF的相似比为1：3，则△ABC和△DEF的面积比为（ ）
| A． | 1：$\sqrt{3}$ | B． | $\sqrt{3}$：1 | C． | 9：1 | D． | 1：9 |
将正整数按如图所示的规律排列下去，若用有序数对（m，n）表示从上到下第m排，从左到右第n个数，如（4，2）表示整数8，则（11，5）表示的数是60．