题目内容
1.在一个不透明的袋子中装有除颇色外其它均相同的m个红球,2个黑球和1个白球.(1)若从中任意取出1个球,取到黑球的概率为$\frac{1}{3}$,则m的值为3.
(2)当m=2时,若从中一次任意摸出2个球,利用树状图或列表法求摸出的2个球颐色相同的概率;
(3)若从中一次任意摸出的2个球颜色不相同的概率为$\frac{5}{9}$,则m的值为6.
分析 (1)根据概率公式得到$\frac{2}{m+2+1}$=$\frac{1}{3}$,然后解方程即可;
(2)画树状图展示所有20种等可能的结果数,找出2个球颐色相同的结果数,然后根据概率公式求解;
(3)从中一次任意摸出的2个球颜色不相同的概率为$\frac{5}{9}$,则从中一次任意摸出的2个球颜色相同的概率为$\frac{4}{9}$,利用(2)中的方法可得共有(m+3-1)(m+3)种可能的结果数,其中2个球颜色相同的结果数为m(m-1)+2,根据概率公式得到$\frac{m(m-1)}{(m+3-1)(m+3)}$=$\frac{4}{9}$,然后解方程即可.
解答 解:(1)根据题意得$\frac{2}{m+2+1}$=$\frac{1}{3}$,解得m=3;
(2)画树状图为:
共有20种等可能的结果数,其中2个球颐色相同的结果数为4,
所以摸出的2个球颐色相同的概率=$\frac{4}{20}$=$\frac{1}{5}$;
(3)从中一次任意摸出的2个球颜色不相同的概率为$\frac{5}{9}$,则从中一次任意摸出的2个球颜色相同的概率为$\frac{4}{9}$,共有(m+3-1)(m+3)种可能的结果数,其中2个球颜色相同的结果数为m(m-1)+2,
根据题意得$\frac{m(m-1)}{(m+3-1)(m+3)}$=$\frac{4}{9}$,解得m=-$\frac{1}{5}$(舍去)或m=6.
故答案为3,6.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
6.方程组$\left\{\begin{array}{l}{x-z=4}\\{z-2y=-1}\\{x+y-z=-1}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=7}\\{y=-5}\\{z=-11}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-7}\\{y=5}\\{z=-11}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-7}\\{y=-5}\\{z=-11}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=7}\\{y=-5}\\{z=11}\end{array}\right.$ |
13.2016年2月3日,广州恒大淘宝足球俱乐部官方宣布与西甲传统劲旅马德里竞技队神锋、哥伦比亚现役国脚马丁内斯正式签约,转会费为4200万欧元(约合人民币3.1亿元),签约四年,其中人民币3.1亿元用科学记数法可以表示为( )元.
| A. | 3.1×107 | B. | 3.1×108 | C. | 31×107 | D. | 0.31×109 |
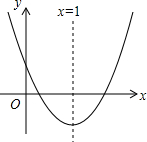 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与y轴的正半轴相交,顶点在第四象限,下列结论:①am2+bm=a(2-m)2+b(2-m);②a+b<0;③$\frac{c}{a}$<1,其中正确的结论个数为( )
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与y轴的正半轴相交,顶点在第四象限,下列结论:①am2+bm=a(2-m)2+b(2-m);②a+b<0;③$\frac{c}{a}$<1,其中正确的结论个数为( )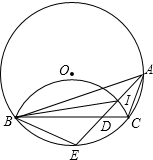 如图,已知△ABC内接于⊙O,点E在弧BC上,AE交BC于点D,EB2=ED•EA经过B、C两点的圆弧交AE于I.
如图,已知△ABC内接于⊙O,点E在弧BC上,AE交BC于点D,EB2=ED•EA经过B、C两点的圆弧交AE于I.