题目内容
20.某商店销售A、B两种商品,部分销售记录如表所示:| 日期 | A商品 | B商品 | 金额 |
| 周一 | 80件 | 50件 | 2850元 |
| 周二 | 40件 | 70件 | 2550元 |
(2)该商店为了促销,推出会员卡业务:先付200元办理一张会员卡,凭会员卡在该商店购买商品可以获得8折优惠.若小王购买会员卡并用此卡按需购买A、B两种商品共100件,共用了y元,设A商品买了x件,请求出y与x的函数关系式;
(3)在(2)的条件下,如果小王利用办会员卡购买这100件商品共用了2000元,那么此次购买比不办会员卡购买节省了多少钱?
分析 (1)根据题意可以列出相应的方程组,从而可以解答本题;
(2)根据题意可以得到y与x的函数关系式;
(3)根据题意可以计算出不买会员卡的花费,从而可以求得此次购买比不办会员卡购买节省了多少钱.
解答 解:(1)设A种商品的单价为x元,B种商品的单价为y元,
$\left\{\begin{array}{l}{80x+50y=2850}\\{40x+70y=2550}\end{array}\right.$,得$\left\{\begin{array}{l}{x=20}\\{y=25}\end{array}\right.$,
即A、B两种商品的单价分别为20元,25元;
(2)由题意可得,
y与x的函数关系式是:y=200+[20x+25(100-x)]×0.8=-4x+2200,
即y与x的函数关系式是y=-4x+2200;
(3)当y=2000时,
2000=-4x+2200,
解得,x=50,
∴不买优惠卡花费为:50×20+(100-50)×25=1000+1250=2250(元),
∵2250-2000=250,
∴此次购买比不办会员卡购买节省了250元.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质解答.

练习册系列答案
相关题目
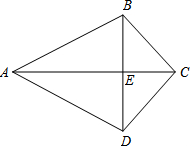 如图,已知△ABC.按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD.
如图,已知△ABC.按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD.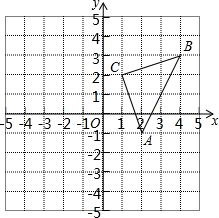 如图,直角坐标系中,△ABC的顶点都在网格点上.其中,A点坐标为(2,-1),将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1,
如图,直角坐标系中,△ABC的顶点都在网格点上.其中,A点坐标为(2,-1),将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1,