题目内容
5.计算:(1)(x-3)2=2x(3-x);(因式分解法)
(2)2y2+5y=7.(公式法)
(3)y2-4y+3=0(配方法)
分析 (1)移项后提取公因式x-3,再求解可得;
(2)整理成一般式,套用求根公式求解可得;
(3)移项后,两边都加上4配成完全平方式,再开方求解可得.
解答 解:(1)∵(x-3)2+2x(x-3)=0,
∴(x-3)(x-3+2x)=0,即(x-3)(3x-3)=0,
则x-3=0或3x-3=0,
解得:x=3或x=1;
(2)原方程整理成一般式可得2y2+5y-7=0,
∵a=2,b=5,c=-7,
∴△=25-4×2×(-7)=81>0,
则y=$\frac{-5±9}{4}$,
∴y=1或y=-$\frac{7}{2}$;
(3)∵y2-4y=-3,
∴y2-4y+4=-3+4,即(y-2)2=1,
则y-2=1或y-2=-1,
解得:y=3或y=1.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
20.某商店销售A、B两种商品,部分销售记录如表所示:
(1)求A、B两种商品的单价;
(2)该商店为了促销,推出会员卡业务:先付200元办理一张会员卡,凭会员卡在该商店购买商品可以获得8折优惠.若小王购买会员卡并用此卡按需购买A、B两种商品共100件,共用了y元,设A商品买了x件,请求出y与x的函数关系式;
(3)在(2)的条件下,如果小王利用办会员卡购买这100件商品共用了2000元,那么此次购买比不办会员卡购买节省了多少钱?
| 日期 | A商品 | B商品 | 金额 |
| 周一 | 80件 | 50件 | 2850元 |
| 周二 | 40件 | 70件 | 2550元 |
(2)该商店为了促销,推出会员卡业务:先付200元办理一张会员卡,凭会员卡在该商店购买商品可以获得8折优惠.若小王购买会员卡并用此卡按需购买A、B两种商品共100件,共用了y元,设A商品买了x件,请求出y与x的函数关系式;
(3)在(2)的条件下,如果小王利用办会员卡购买这100件商品共用了2000元,那么此次购买比不办会员卡购买节省了多少钱?
15.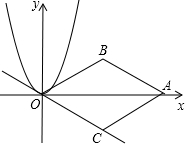 如图,在平面直角坐标系中,点A(4$\sqrt{3}$,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC=60°,现将抛物线y=x2沿直线OC平移到y=a(x-m)2+h,则当抛物线与菱形的AB边有公共点时,则m的取值范围是( )
如图,在平面直角坐标系中,点A(4$\sqrt{3}$,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC=60°,现将抛物线y=x2沿直线OC平移到y=a(x-m)2+h,则当抛物线与菱形的AB边有公共点时,则m的取值范围是( )
 如图,在平面直角坐标系中,点A(4$\sqrt{3}$,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC=60°,现将抛物线y=x2沿直线OC平移到y=a(x-m)2+h,则当抛物线与菱形的AB边有公共点时,则m的取值范围是( )
如图,在平面直角坐标系中,点A(4$\sqrt{3}$,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC=60°,现将抛物线y=x2沿直线OC平移到y=a(x-m)2+h,则当抛物线与菱形的AB边有公共点时,则m的取值范围是( )| A. | $\sqrt{3}$≤m≤3$\sqrt{3}$ | B. | 3$\sqrt{3}$≤m≤$\frac{10}{3}$$\sqrt{3}$ | C. | $\frac{10}{3}$$\sqrt{3}$≤m≤$\frac{16}{3}$$\sqrt{3}$ | D. | $\sqrt{3}$≤m≤$\frac{16}{3}$$\sqrt{3}$ |
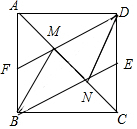 如图,在正方形ABCD,M、N是对角线AC上的两点,且AM=CN,连接DM并延长,交AB于点F,连接BN并延长,交DC于点E.连接BM、DN.
如图,在正方形ABCD,M、N是对角线AC上的两点,且AM=CN,连接DM并延长,交AB于点F,连接BN并延长,交DC于点E.连接BM、DN.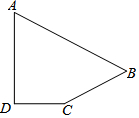 在四边形ABCD中,∠D=90°,AD=$\sqrt{12}$,CD=2,BC=3,AB=5,求:四边形ABCD的面积.
在四边形ABCD中,∠D=90°,AD=$\sqrt{12}$,CD=2,BC=3,AB=5,求:四边形ABCD的面积.