题目内容
15.(1)cos60°+$\frac{\sqrt{2}}{2}$sin45°+tan30°•cos30°;(2)$\sqrt{ta{n}^{2}60°-4tan60°+4}$-$\frac{2\sqrt{2}tan45°}{tan60°-tan45°}$.
分析 (1)根据特殊角三角函数值,可得答案;
(2)根据特殊角三角函数值,可得答案.
解答 解:(1)原式=$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{3}$×$\frac{\sqrt{3}}{2}$
=$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$+$\frac{1}{2}$
=$\frac{\sqrt{3}+2}{2}$;
(2)原式=$\sqrt{(\sqrt{3})^{2}-4×\sqrt{3}+4}$-$\frac{2\sqrt{2}×1}{\frac{\sqrt{3}}{3}-1}$
=2-$\sqrt{3}$+$\sqrt{6}$+3$\sqrt{2}$.
点评 本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题关键.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
6.△ABC中,∠A=∠B+∠C,则对△ABC的形状判断正确的是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等边三角形 |
20.某商店销售A、B两种商品,部分销售记录如表所示:
(1)求A、B两种商品的单价;
(2)该商店为了促销,推出会员卡业务:先付200元办理一张会员卡,凭会员卡在该商店购买商品可以获得8折优惠.若小王购买会员卡并用此卡按需购买A、B两种商品共100件,共用了y元,设A商品买了x件,请求出y与x的函数关系式;
(3)在(2)的条件下,如果小王利用办会员卡购买这100件商品共用了2000元,那么此次购买比不办会员卡购买节省了多少钱?
| 日期 | A商品 | B商品 | 金额 |
| 周一 | 80件 | 50件 | 2850元 |
| 周二 | 40件 | 70件 | 2550元 |
(2)该商店为了促销,推出会员卡业务:先付200元办理一张会员卡,凭会员卡在该商店购买商品可以获得8折优惠.若小王购买会员卡并用此卡按需购买A、B两种商品共100件,共用了y元,设A商品买了x件,请求出y与x的函数关系式;
(3)在(2)的条件下,如果小王利用办会员卡购买这100件商品共用了2000元,那么此次购买比不办会员卡购买节省了多少钱?
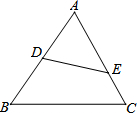 已知:如图,在△ABC中,AD=12,EC=2,BD=12,AE=16,求证:△ADE∽△ACB.
已知:如图,在△ABC中,AD=12,EC=2,BD=12,AE=16,求证:△ADE∽△ACB.