题目内容
8.已知在平面直角坐标系中,A(0,4),B(7,3).(1)点P在x轴上,且PA=PB,求P的坐标.
(2)点Q在x轴上,且QA+QB最短,求QA+QB的最小值.
分析 (1)如图1,连接AB,作AB的垂直平分线交x轴于P,则PA=PB,根据已知条件得到直线AB的解析式为:y=-$\frac{1}{7}$x+4,AB的中点坐标为(3.5,3.5),得到AB的垂直平分线的解析式为y=7x-21,于是得到结论;
(2)作A关于x轴的对称点A′,连接A′B交x轴于Q,则A′B=QA+QB的最小值,过B作BH⊥AA′于H,解直角三角形即可得到结论.
解答  解:(1)如图1,连接AB,作AB的垂直平分线交x轴于P,则PA=PB,
解:(1)如图1,连接AB,作AB的垂直平分线交x轴于P,则PA=PB,
∵A(0,4),B(7,3),
∴直线AB的解析式为:y=-$\frac{1}{7}$x+4,AB的中点坐标为(3.5,3.5),
设AB的垂直平分线的解析式为y=7x+b,
把(3.5,3.5)代入y=7x+b得,b=21,
∴AB的垂直平分线的解析式为y=7x-21,
当y=0时,x=3,
∴P(3,0);
(2)作A关于x轴的对称点A′,连接A′B交x轴于Q,
则A′B=QA+QB的最小值,
过B作BH⊥AA′于H,
∴A′H=7,BH=7,
∴A′B=7$\sqrt{2}$,
∴QA+QB的最小值是7$\sqrt{2}$.
点评 本题考查了轴对称-最短路线问题,线段垂直平分线的性质,勾股定理,关键是找出P,Q点的位置,题目比较好,难度适中.

练习册系列答案
相关题目
20.某商店销售A、B两种商品,部分销售记录如表所示:
(1)求A、B两种商品的单价;
(2)该商店为了促销,推出会员卡业务:先付200元办理一张会员卡,凭会员卡在该商店购买商品可以获得8折优惠.若小王购买会员卡并用此卡按需购买A、B两种商品共100件,共用了y元,设A商品买了x件,请求出y与x的函数关系式;
(3)在(2)的条件下,如果小王利用办会员卡购买这100件商品共用了2000元,那么此次购买比不办会员卡购买节省了多少钱?
| 日期 | A商品 | B商品 | 金额 |
| 周一 | 80件 | 50件 | 2850元 |
| 周二 | 40件 | 70件 | 2550元 |
(2)该商店为了促销,推出会员卡业务:先付200元办理一张会员卡,凭会员卡在该商店购买商品可以获得8折优惠.若小王购买会员卡并用此卡按需购买A、B两种商品共100件,共用了y元,设A商品买了x件,请求出y与x的函数关系式;
(3)在(2)的条件下,如果小王利用办会员卡购买这100件商品共用了2000元,那么此次购买比不办会员卡购买节省了多少钱?
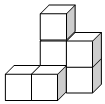 如图所示的几何体是由相同的小正方体搭成的,请画出它的主视图、左视图和俯视图.
如图所示的几何体是由相同的小正方体搭成的,请画出它的主视图、左视图和俯视图.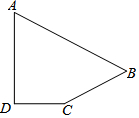 在四边形ABCD中,∠D=90°,AD=$\sqrt{12}$,CD=2,BC=3,AB=5,求:四边形ABCD的面积.
在四边形ABCD中,∠D=90°,AD=$\sqrt{12}$,CD=2,BC=3,AB=5,求:四边形ABCD的面积.