题目内容
12.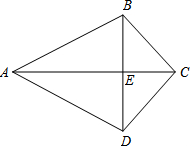 如图,已知△ABC.按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD.
如图,已知△ABC.按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD.(1)求证:△ABC≌△ADC;
(2)若∠BAC=30°,∠BCA=45°,AC=$\sqrt{3}$+1,求BE的长.
分析 (1)根据作图以及公共边,运用SSS可以证明△ABC≌△ADC;
(2)根据等腰三角形三线合一的性质证明△AEB是直角三角形,根据△BCE是等腰直角三角形,可得BE=CE,最后设BE=CE=x,则AE=$\sqrt{3}$x,依据AC=$\sqrt{3}$+1,列出方程求解即可.
解答  解:(1)在△ABC与△ADC中,
解:(1)在△ABC与△ADC中,
$\left\{\begin{array}{l}{AB=AD}\\{BC=CD}\\{AC=AC}\end{array}\right.$,
∴△ABC≌△ADC(SSS);
(2)∵△ABC≌△ADC,
∴∠BAE=∠DAE,
又∵AB=AD,
∴AE⊥BD,
∴∠AEB=∠AED=90°,
∵∠BAC=30°,
∴AE=$\sqrt{3}$BE,
又∵∠BCA=45°,
∴△BCE是等腰直角三角形,
∴BE=CE,
设BE=CE=x,则AE=$\sqrt{3}$x,
∵AC=$\sqrt{3}$+1,
∴$\sqrt{3}$x+x=$\sqrt{3}$+1,
解得x=1,
∴BE=1.
点评 本题主要考查了全等三角形的判定与性质以及直角三角形的性质的运用,解题时注意:三条边分别对应相等的两个三角形全等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.某商店销售A、B两种商品,部分销售记录如表所示:
(1)求A、B两种商品的单价;
(2)该商店为了促销,推出会员卡业务:先付200元办理一张会员卡,凭会员卡在该商店购买商品可以获得8折优惠.若小王购买会员卡并用此卡按需购买A、B两种商品共100件,共用了y元,设A商品买了x件,请求出y与x的函数关系式;
(3)在(2)的条件下,如果小王利用办会员卡购买这100件商品共用了2000元,那么此次购买比不办会员卡购买节省了多少钱?
| 日期 | A商品 | B商品 | 金额 |
| 周一 | 80件 | 50件 | 2850元 |
| 周二 | 40件 | 70件 | 2550元 |
(2)该商店为了促销,推出会员卡业务:先付200元办理一张会员卡,凭会员卡在该商店购买商品可以获得8折优惠.若小王购买会员卡并用此卡按需购买A、B两种商品共100件,共用了y元,设A商品买了x件,请求出y与x的函数关系式;
(3)在(2)的条件下,如果小王利用办会员卡购买这100件商品共用了2000元,那么此次购买比不办会员卡购买节省了多少钱?
1.一汽车的速度是每小时60千米,一次加满油可加40升,每小时耗油5升,t小时后行程S千米.
(1)写出一次加满油后所行路程S与时间t的函数关系式.
(2)求出自变量的取值范围.
(3)画出这个函数的图象.
(1)写出一次加满油后所行路程S与时间t的函数关系式.
(2)求出自变量的取值范围.
(3)画出这个函数的图象.
2.如果关于x的一元二次方程x2-6x+m=0有两个相等的实数根,则m所满足的条件是( )
| A. | m<9 | B. | m>9 | C. | m=9 | D. | m≤9 |
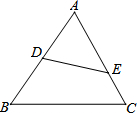 已知:如图,在△ABC中,AD=12,EC=2,BD=12,AE=16,求证:△ADE∽△ACB.
已知:如图,在△ABC中,AD=12,EC=2,BD=12,AE=16,求证:△ADE∽△ACB.