题目内容
10.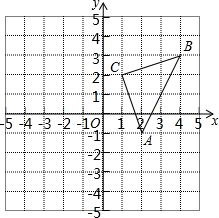 如图,直角坐标系中,△ABC的顶点都在网格点上.其中,A点坐标为(2,-1),将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1,
如图,直角坐标系中,△ABC的顶点都在网格点上.其中,A点坐标为(2,-1),将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1,(1)画出平移后的图形;
(2)写出A1、B1、C1的坐标;、
(3)求△A1B1C1的面积.
分析 (1)根据图形平移的性质画出△A1B1C1即可;
(2)根据各点在坐标系中的位置写出各点坐标即可;
(3)利用矩形的面积减去三个顶点上三角形的面积即可.
解答  解:(1)如图,△A1B1C1即为所求;
解:(1)如图,△A1B1C1即为所求;
(2)由图可知,A1(5,-3),B1(7,1),C1(4,0);
(3)△A1B1C1的面积=3×4-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×4
=12-$\frac{3}{2}$-$\frac{3}{2}$-4
=5.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
相关题目
20.某商店销售A、B两种商品,部分销售记录如表所示:
(1)求A、B两种商品的单价;
(2)该商店为了促销,推出会员卡业务:先付200元办理一张会员卡,凭会员卡在该商店购买商品可以获得8折优惠.若小王购买会员卡并用此卡按需购买A、B两种商品共100件,共用了y元,设A商品买了x件,请求出y与x的函数关系式;
(3)在(2)的条件下,如果小王利用办会员卡购买这100件商品共用了2000元,那么此次购买比不办会员卡购买节省了多少钱?
| 日期 | A商品 | B商品 | 金额 |
| 周一 | 80件 | 50件 | 2850元 |
| 周二 | 40件 | 70件 | 2550元 |
(2)该商店为了促销,推出会员卡业务:先付200元办理一张会员卡,凭会员卡在该商店购买商品可以获得8折优惠.若小王购买会员卡并用此卡按需购买A、B两种商品共100件,共用了y元,设A商品买了x件,请求出y与x的函数关系式;
(3)在(2)的条件下,如果小王利用办会员卡购买这100件商品共用了2000元,那么此次购买比不办会员卡购买节省了多少钱?
1.一汽车的速度是每小时60千米,一次加满油可加40升,每小时耗油5升,t小时后行程S千米.
(1)写出一次加满油后所行路程S与时间t的函数关系式.
(2)求出自变量的取值范围.
(3)画出这个函数的图象.
(1)写出一次加满油后所行路程S与时间t的函数关系式.
(2)求出自变量的取值范围.
(3)画出这个函数的图象.
15.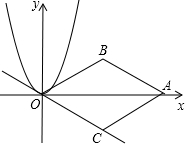 如图,在平面直角坐标系中,点A(4$\sqrt{3}$,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC=60°,现将抛物线y=x2沿直线OC平移到y=a(x-m)2+h,则当抛物线与菱形的AB边有公共点时,则m的取值范围是( )
如图,在平面直角坐标系中,点A(4$\sqrt{3}$,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC=60°,现将抛物线y=x2沿直线OC平移到y=a(x-m)2+h,则当抛物线与菱形的AB边有公共点时,则m的取值范围是( )
 如图,在平面直角坐标系中,点A(4$\sqrt{3}$,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC=60°,现将抛物线y=x2沿直线OC平移到y=a(x-m)2+h,则当抛物线与菱形的AB边有公共点时,则m的取值范围是( )
如图,在平面直角坐标系中,点A(4$\sqrt{3}$,0)是x轴上一点,以OA为对角线作菱形OBAC,使得∠BOC=60°,现将抛物线y=x2沿直线OC平移到y=a(x-m)2+h,则当抛物线与菱形的AB边有公共点时,则m的取值范围是( )| A. | $\sqrt{3}$≤m≤3$\sqrt{3}$ | B. | 3$\sqrt{3}$≤m≤$\frac{10}{3}$$\sqrt{3}$ | C. | $\frac{10}{3}$$\sqrt{3}$≤m≤$\frac{16}{3}$$\sqrt{3}$ | D. | $\sqrt{3}$≤m≤$\frac{16}{3}$$\sqrt{3}$ |
2.如果关于x的一元二次方程x2-6x+m=0有两个相等的实数根,则m所满足的条件是( )
| A. | m<9 | B. | m>9 | C. | m=9 | D. | m≤9 |



