题目内容
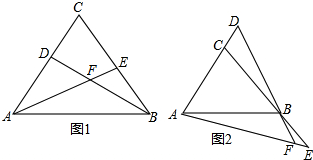
 如图,等腰△ABC中,AC=BC,△BDC和△ACE分别为等边三角形,AE与BD相交于点F,连接CF并延长,交AB于点G.求证:G为AB的中点.
如图,等腰△ABC中,AC=BC,△BDC和△ACE分别为等边三角形,AE与BD相交于点F,连接CF并延长,交AB于点G.求证:G为AB的中点.考点:全等三角形的判定与性质,等腰三角形的性质,等边三角形的性质
专题:证明题
分析:求证△AFC≌△CEB可得∠ACF=∠BCF,根据等腰三角形底边三线合一即可解题.
解答:证明:∵CA=CB
∴∠CAB=∠CBA
∵△AEC和△BCD为等边三角形
∴∠CAE=∠CBD,∠FAG=∠FBG
∴AF=BF.
在三角形ACF和△CBF中,
,
∴△AFC≌△CEB(SSS),
∴∠ACF=∠BCF
∴AG=BG(三线合一)
∴G为AB的中点
∴∠CAB=∠CBA
∵△AEC和△BCD为等边三角形
∴∠CAE=∠CBD,∠FAG=∠FBG
∴AF=BF.
在三角形ACF和△CBF中,
|
∴△AFC≌△CEB(SSS),
∴∠ACF=∠BCF
∴AG=BG(三线合一)
∴G为AB的中点
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,考查了等腰三角形底边三线合一的性质.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
下列各式错误的是( )
| A、1-(+5)=-4 |
| B、0-(+3)=-3 |
| C、(+6)-(-6)=0 |
| D、(-15)-(-5)=-10 |
 如图,在☉O中直径为AB=10,弦CD⊥AB,垂足为点E,OE=3,弦CD的长是
如图,在☉O中直径为AB=10,弦CD⊥AB,垂足为点E,OE=3,弦CD的长是 已知:如图,AB=DC,AE=BF,CE=DF,∠A=60°.
已知:如图,AB=DC,AE=BF,CE=DF,∠A=60°.