题目内容

19．已知△ABC中，∠A=$\frac{1}{2}$∠B，∠B=$\frac{1}{3}$∠C，求△ABC的各个内角的度数，并判断它是什么三角形．

分析 根据三角形内角和定理列出关于∠A的方程，求出∠A的值即可．

解答 解：根据题意有：
∠B=2∠A  ①；∠C=3∠B  ②
可得∠C=6∠A③
把①和③代入∠A+∠B+∠C=180中，
9∠A=180°，
解得：∠A=20°，可得：∠B=40°，∠C=120°
因此△ABC是钝角三角形．

点评 本题涉及到三角形内角和定理问题，关键是根据三角形内角和定理列出关于∠A的方程．

练习册系列答案
相关题目
9．认真阅读下面的材料，完成有关问题．
材料1：在学习绝对值时，老师教过我们绝对值的几何含义，如|5-3|表示5、3在数轴上对应的两点之间的距离；|5+3|=|5-（-3）|，所以|5+3|表示5、-3在数轴上对应的两点之间的距离；|5|=|5-0|，所以|5|表示5在数轴上对应的点到原点的距离．一般地，点A、B在数轴上分别表示有理数a、b，那么A、B之间的距离可表示为|a-b|．
问题（1）：点A、B、C在数轴上分别表示有理数x、-2、1，那么A到B的距离与A到C的距离之和可表示为|x+2|+|x-1| （用含绝对值的式子表示）．
问题（2）：利用数轴探究：
①找出满足|x-3|+|x+1|=6的x的所有值是-2，4，
②设|x-3|+|x+1|=p，当x的值取在不小于-1且不大于3的范围时，p的值是不变的，而且是p的最小值，这个最小值是4；当x的值取在不小于0且不大于2 的范围时，|x|+|x-2|的最小值是2

材料2：求|x-3|+|x-2|+|x+1|的最小值．
分析：|x-3|+|x-2|+|x+1|=（|x-3|+|x+1|）+|x-2|
根据问题（2）中的探究②可知，要使|x-3|+|x+1|的值最小，x的值只要取-1到3之间（包括-1、3）的任意一个数，要使|x-2|的值最小，x应取2，显然当x=2时能同时满足要求，把x=2代入原式计算即可．
问题（3）：利用材料2的方法求出|x-3|+|x-2|+|x|+|x+1|的最小值．
10．把下列各数填在相应的大括号里：
$\frac{3}{4}$，0.86，-|-2|，-（-2），0，-$\frac{10}{3}$，1$\frac{1}{4}$，3.14，
负整数集合：（-|-2| …）；负分数集合：（-$\frac{10}{3}$…）；负有理数集合：（-|-2|，-$\frac{10}{3}$ …）．
7．如图，经测量石拱桥的桥顶到水面的距离CD为8m，水面宽AB为8cm，则桥拱半径为多少？
14．若函数y=x2的图象经过A（a-1，y1）、B（a，y2）、c（a+1，y3）三点，且a＜-1，则（　　）
A．y1＜y2＜y3B．y1＜y3＜y2C．y3＜y2＜y3D．y2＜y1＜y3
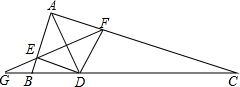4．如图，在△ABC中，AC=3AB，AD平分∠BAC，交BC边于点D，DE∥CA，交AB边于点E，DF∥BA，交AC边于点F，FE的延长线与CB的延长线交于点G．
（1）求证：EF=2EG；
（2）求S△GBE：S△ABC．
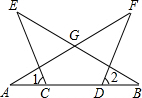11．如图，已知：CE=DF，AC=BD，∠1=∠2．求证：△GAB是等腰三角形．
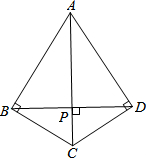8．如图，四边形ABCD中，∠ABC=∠ADC=90°，BD⊥AC，垂足为P．
（1）请作出Rt△ABC的外接圆⊙O；（保留作图痕迹，不写作法）
（2）点D在⊙O上吗？说明理由；
（3）试说明：AC平分∠BAD．
9．填空：
（1）ac＜bc＜0，c＜0，则c-a＜c-b；
（2）$\sqrt{{a}^{2}+3}$＜$\sqrt{{a}^{2}+4}$；
（3）已知a＜b＜0，那么$\frac{a}{b}$＞1；
（4）若a＞c，b＜-c，那么（a-c）（b+c）＜0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网