题目内容
11．
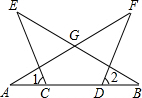如图，已知：CE=DF，AC=BD，∠1=∠2．求证：△GAB是等腰三角形．
分析 利用等式的性质证明CB=AD，再利用SAS证明△ECB与△FDA全等，进而证明即可．
解答 证明：∵AC=BD，
∴AC+CD=DB+CD，
∴AD=BC，
∵∠1=∠2，
∴∠ECB=∠FDA，
在△ECB与△FDA中，
$\left\{\begin{array}{l}{AD=BC}\\{∠ECB=∠FDA}\\{CE=DF}\end{array}\right.$，
∴△ECB≌△FDA（SAS），
∴∠B=∠A，
∴△GAB是等腰三角形．
点评 此题考查全等三角形的判定和性质，关键是利用等式的性质证明CB=AD．
练习册系列答案
激活思维智能训练课时导学练系列答案
相关题目
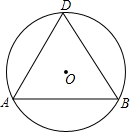如图，已知⊙O的半径为2，弦AB的长为2$\sqrt{3}$，D是优弧$\widehat{ADB}$上的任意一点（点D不与A，B重合）．
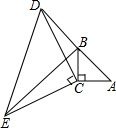如图，在△ABC中，∠ACB=90°，AC=BC，延长AB至点D，使DB=AB，连接CD，以CD为直角边作等腰直角三角形CDE，其中∠DCE=90°，连接BE．