题目内容
9.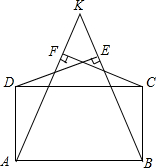 如图,K为矩形ABCD的CD边外的一点,连线KA、KB均与CD边相交,过D作KB的垂线,垂足为E,过C作KA的垂线,垂足为F,若DE、CF交于点M,求证:KM⊥AB.
如图,K为矩形ABCD的CD边外的一点,连线KA、KB均与CD边相交,过D作KB的垂线,垂足为E,过C作KA的垂线,垂足为F,若DE、CF交于点M,求证:KM⊥AB.
分析 如图,连接KM,EF,作矩形ABCD的外接圆,只要证明A、B、C、E、F、D共圆,可得∠DAK=∠DCF=∠DEF=∠MKF,推出AD∥KM,即可解决问题.
解答 解:如图,连接KM,EF,作矩形ABCD的外接圆,
∵四边形ABCD是矩形,
∴A、B、C、D四点共圆,
∵∠ADC=∠AFC=90°,∠DCB=∠DEB=90°,
∴A、D、F、C四点共圆,D、E、C、B四点共圆,
∴A、B、C、E、F、D共圆,
∴∠DAK=∠DCF=∠DEF=∠MKF,
∴AD∥KM,
∵AD⊥AB,
∴KM⊥AB.
点评 本题考查矩形的性质、四点共圆、平行线的判定等知识,解题的关键是发现A、B、C、E、F、D共圆,利用同弧所对的圆周角相等解决问题,题目比较难,属于中考压轴题.

练习册系列答案
相关题目
6.(-0.25)2003×(-4)2002的值是( )
| A. | -0.25 | B. | 4 | C. | -4 | D. | -2 |
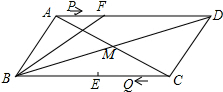 如图,在?ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,△FBM≌△CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动3或5秒时,以P、Q、E、F为顶点的四边形是平行四边形.
如图,在?ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,△FBM≌△CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动3或5秒时,以P、Q、E、F为顶点的四边形是平行四边形.