题目内容
19.(1)计算:$\sqrt{4}$-tan45°+|-1|(2)解方程:$\frac{2{x}^{2}+1}{2x}$=x+1.
分析 (1)本题涉及特殊三角函数值、二次根式化简、绝对值3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=2-1+1=2.
(2)去分母得,2x2+1=2x2+2x,
解得:x=$\frac{1}{2}$,
经检验x=$\frac{1}{2}$是分式方程的解.
点评 此题考查了实数的运算以及解分式方程,熟练掌握负整数指数幂、零指数幂、二次根式、绝对值以及分式方程的解法是本题的关键.

练习册系列答案
相关题目
10.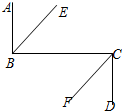 如图,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么∠ABE与∠DCF的位置和大小关系是( )
如图,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么∠ABE与∠DCF的位置和大小关系是( )
 如图,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么∠ABE与∠DCF的位置和大小关系是( )
如图,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么∠ABE与∠DCF的位置和大小关系是( )| A. | 是同位角且相等 | B. | 不是同位角但相等 | ||
| C. | 是同位角但不等 | D. | 不是同位角也不等 |
8.根据下列条件,能判定△ABC≌△A′B′C′的是( )
| A. | AB=A′B′,BC=B′C′,∠A=∠A′ | |
| B. | ∠A=∠A′,∠B=∠B′,AC=B′C′ | |
| C. | ∠A=∠A′,∠B=∠B′,∠C=∠C′ | |
| D. | AB=A′B′,BC=B′C′,△ABC的周长等于△A′B′C′的周长 |
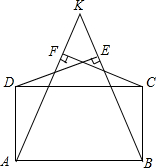 如图,K为矩形ABCD的CD边外的一点,连线KA、KB均与CD边相交,过D作KB的垂线,垂足为E,过C作KA的垂线,垂足为F,若DE、CF交于点M,求证:KM⊥AB.
如图,K为矩形ABCD的CD边外的一点,连线KA、KB均与CD边相交,过D作KB的垂线,垂足为E,过C作KA的垂线,垂足为F,若DE、CF交于点M,求证:KM⊥AB.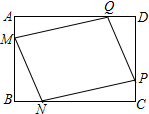 某小区在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化,为了绿化环境又节省成本.如图,已知矩形的边BC=200m,边AB=a m(a为不大于200的常数),四边形MNPQ的顶点在矩形的边上,且AM=BN=CP=DQ=x m,设四边形MNPQ的面积为S m2
某小区在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化,为了绿化环境又节省成本.如图,已知矩形的边BC=200m,边AB=a m(a为不大于200的常数),四边形MNPQ的顶点在矩形的边上,且AM=BN=CP=DQ=x m,设四边形MNPQ的面积为S m2