题目内容
5.某商店购进某种商品的单价为50元,销售单价定为60元时,能卖出500个,预测这种商品每件每涨价1元,其销售量就会减少10件.问:销售单价定为多少元时能获得最大利润?最大利润是多少?分析 利用总利润=销售量×每个利润.设售价为x元,总利润为W元,则销售量为500-10(x-60),每个利润为(x-50),据此表示总利润,再根据函数性质求最大值.
解答 解:设售价为x元,总利润为W元,则W=(x-50)[500-10(x-60)]=-10x2+1600x-55000=-10(x-80)2+9000,
∵-10<0,
∴函数有最大值,
当x=80元时,W最大,最大值为9000元,
答:定价为80元时可获得最大利润,最大利润为9000元.
点评 此题主要考查了二次函数的应用,解题的关键是搞清楚利润、销售量、销售价、进价之间的关系,学会构建二次函数进价最值问题,需要熟练掌握配方法.属于中考常考题型.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
16.投掷一枚均匀的骰子,掷出的点数是3的倍数的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
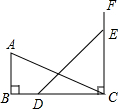 如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,过点C作CF⊥BC,如果点D,E分别在BC、CF上运动,并始终保持DE=EC,那么当CD=6或8时,△ABC与△DCE全等.
如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,过点C作CF⊥BC,如果点D,E分别在BC、CF上运动,并始终保持DE=EC,那么当CD=6或8时,△ABC与△DCE全等. 一次函数y=kx+b的图象如图,则当0≤x≤1时,y的范围是-2≤y<0.
一次函数y=kx+b的图象如图,则当0≤x≤1时,y的范围是-2≤y<0.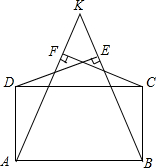 如图,K为矩形ABCD的CD边外的一点,连线KA、KB均与CD边相交,过D作KB的垂线,垂足为E,过C作KA的垂线,垂足为F,若DE、CF交于点M,求证:KM⊥AB.
如图,K为矩形ABCD的CD边外的一点,连线KA、KB均与CD边相交,过D作KB的垂线,垂足为E,过C作KA的垂线,垂足为F,若DE、CF交于点M,求证:KM⊥AB.