题目内容
15.抛物线y=-x2+bx+c与x轴交于点A(3,0)、B(0,3)与y轴交于点B.(1)求抛物线的解析式;
(2)点P为第一象限的抛物线上一动点,OP交AB于点C,若PC:OC=2:3,求点P的坐标;
(3)若点P是抛物线上的动点,点Q是x轴上的动点,判断有几个位置能使以P、Q、A、B为顶点的四边形为平行四边形,直接写出相应的点P的坐标.
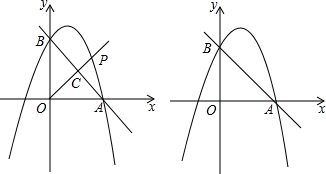
分析 (1)只需把点A、B的坐标代入抛物线的解析式,就可解决问题;
(2)过点C作CM⊥x轴于M,过点P作PN⊥x轴于N,如图所示,设点P的坐标为(m,n),则ON=m,PN=n.易证△OMC∽△ONP,根据相似三角形的性质可得OM=$\frac{3}{5}$m,CM=$\frac{3}{5}$n.易得MA=CM=$\frac{3}{5}$n,从而可得n=5-m,然后把点P(m,5-m)代入抛物线的解析式,就可解决问题;
(3)由于AB确定,可分AB是平行四边形的边和对角线两种情况讨论,得到点P与点B的纵坐标之间的关系,然后代入抛物线的解析式,就可解决问题.
解答 解:(1)∵A(3,0)、B(0,3)在抛物线y=-x2+bx+c上,
$\left\{\begin{array}{l}{-9+3b+c=0}\\{c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$.
∴抛物线的解析式为y=-x2+2x+3;
(2)过点C作CM⊥x轴于M,过点P作PN⊥x轴于N,如图所示,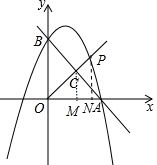
则有CM∥PN,
∴△OMC∽△ONP,
∴$\frac{OM}{ON}$=$\frac{CM}{PN}$=$\frac{OC}{OP}$.
设点P的坐标为(m,n),
则ON=m,PN=n.
∵PC:OC=2:3,
∴$\frac{OC}{OP}$=$\frac{3}{5}$,
∴$\frac{OM}{m}$=$\frac{CM}{n}$=$\frac{3}{5}$,
∴OM=$\frac{3}{5}$m,CM=$\frac{3}{5}$n.
∵OA=OB=3,∠AOB=90°,
∴∠OAB=45°,
∴MA=CM=$\frac{3}{5}$n,
∴$\frac{3}{5}$m+$\frac{3}{5}$n=3,
∴n=5-m,
∴点P的坐标为(m,5-m),
∴5-m=-m2+2m+3,
整理得m2-3m+2=0,
解得m1=2,m2=1.
当m=2时,点P的坐标为(2,3);
当m=1时,点P的坐标为(1,4).
则点P的坐标为(2,3)和(1,4);
(3)①若AB为平行四边形的一边,
则P、B到AQ的距离相等,
∴|yP|=|yB|=3,
∴yP=±3.
当yP=3时,解方程-x2+2x+3=3得,
x1=0,x2=2,
∴点P的坐标为(2,3);
当yP=-3时,解方程-x2+2x+3=-3得,
x1=1-$\sqrt{7}$,x2=1+$\sqrt{7}$,
∴点P的坐标为(1-$\sqrt{7}$,-3)或(1+$\sqrt{7}$,-3);
②若AB为平行四边形的一条对角线,
则BP∥AQ,
∴yP=yB=3,
∴点P的坐标为(2,3).
综上所述:满足条件的点P的坐标为(2,3)、(1-$\sqrt{7}$,-3)或(1+$\sqrt{7}$,-3).
点评 本题主要考查了运用待定系数法求抛物线的解析式、抛物线上点的坐标特征、解一元二次方程、平行四边形的性质、抛物线的性质等知识,构造相似三角形是解决第(2)小题的关键,运用分类讨论的思想是解决第(3)小题的关键.

| A. | x>2 | B. | x>3 | C. | x≠2 | D. | x≠3 |
| A. | m≤3 | B. | m<3 | C. | m≥3 | D. | m>3 |
 如图,把一个长方形纸条ABCD沿EF折叠,若∠1=55°,则∠AEG=70.
如图,把一个长方形纸条ABCD沿EF折叠,若∠1=55°,则∠AEG=70.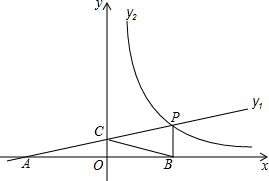 如图所示,直线y1=$\frac{1}{4}x+1$与x轴交于点A,与y轴交于点C,与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于点P,作PB⊥x轴于点B,且AC=BC.
如图所示,直线y1=$\frac{1}{4}x+1$与x轴交于点A,与y轴交于点C,与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于点P,作PB⊥x轴于点B,且AC=BC.