Question

19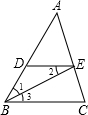．如图所示，已知BE平分∠ABC，∠1=∠2，求证：∠AED=∠C．完善以下推理过程．
证明：∵BE平分∠ABC，∴∠1=∠3． （已知）
又∵∠1=∠2（已知），∴∠2=∠3（ 等量代换），
∴DE∥BC（内错角相等，两直线平行）
∴∠AED=∠C （两直线平行，同位角相等）．

Answer 1

分析 先根据等量代换，得出∠2=∠3，再根据平行线的判定，得出DE∥BC，最后根据平行线的性质，得出∠AED=∠C．

解答 证明：∵BE平分∠ABC，
∴∠1=∠3（角平分线定义），
又∵∠1=∠2（已知），
∴∠2=∠3（等量代换），
∴DE∥BC（内错角相等，两直线平行），
∴∠AED=∠C（两直线平行，同位角相等）．
故答案为：已知，∠2，∠3，DE，BC，内错角相等，两直线平行，两直线平行，同位角相等．

点评 本题主要考查了平行线的性质与判定，平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．