题目内容
10.已知x≠1,计算(1-x)(1+x)=1-x2,
(1-x)(1+x+x2)=1-x3,
(1-x)(1+x+x2+x3)=1-x4.
(1)观察以上各式并猜想:(1-x)(1+x+x2+…+xn)=1-xn+1(n为正整数);
(2)根据你的猜想计算:
(1-2)(1+2+22+23+…+299)=1-2100;
2+22+23+…+2n=2n+1-2.
(x-1)(x99+x98+x97+…+x2+x+1)=x100-1.
分析 (1)归纳总结得到一般性规律,写出即可;
(2)①根据得出的规律计算即可得到结果;
②原式变形后,利用得出的规律计算即可得到结果;
③原式变形后,利用得出的规律计算即可得到结果.
解答 解:(1)(1-x)(1+x+x2+…+xn)=1-xn+1;
(2)①原式=1-2100;
②原式=2(1+2+22+…+2n-1)=-2(1-2)(1+2+22+…+2n-1)=-2(1-2n)=2n+1-2;
③原式=-(1-x)(x99+x98+x97+…+x2+x+1)=-1+x100.
故答案为:(1)1-xn+1
(2)1-2100
2n+1-2
x100-1
点评 此题考查了整式混合运算的应用,找出其中的规律是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.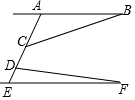 如图,AB∥EF,∠BCD=135°,∠FDC=85°,则∠B+∠F的度数为( )
如图,AB∥EF,∠BCD=135°,∠FDC=85°,则∠B+∠F的度数为( )
 如图,AB∥EF,∠BCD=135°,∠FDC=85°,则∠B+∠F的度数为( )
如图,AB∥EF,∠BCD=135°,∠FDC=85°,则∠B+∠F的度数为( )| A. | 38° | B. | 40° | C. | 55° | D. | 60° |
20.直线y=3x+6与y=2x-4的交点坐标为( )
| A. | (10,-24) | B. | (-10,-24) | C. | (10,24) | D. | (-10,24) |

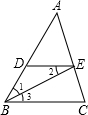 如图所示,已知BE平分∠ABC,∠1=∠2,求证:∠AED=∠C.完善以下推理过程.
如图所示,已知BE平分∠ABC,∠1=∠2,求证:∠AED=∠C.完善以下推理过程.