题目内容
14．
如图，在平行四边形ABCD中，BE⊥AB于B，BE交对角线AC于E，∠ACD=15°，求∠BEC的值．
分析 首先由在?ABCD中，∠ACD=15°，求得∠BAE的度数，然后由BE⊥AB，利用三角形外角的性质，求得∠BEC的度数．
解答 解：∵四边形ABCD是平行四边形，
∴CD∥AB，
∴∠CAB=15°，
∴∠BEC=∠CAB+∠ABE=15°+90°=105°．
点评 此题考查了平行四边形的性质以及三角形外角的性质．熟练掌握平行四边形的性质是解决问题的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
4．下列各式中计算正确的是（ ）
| A． | $\sqrt{（-4）（-16）}$=$\sqrt{-4}$$•\sqrt{-16}$=（-2）（-4）=8 | B． | $\sqrt{8{a}^{2}}$=4a（a≥0） | ||
| C． | $\sqrt{4{1}^{2}-4{0}^{2}}$=$\sqrt{41+40}$$•\sqrt{41-40}$=9×1=9 | D． | $\sqrt{{3}^{2}+{4}^{2}}$=3+4=7 |
已知：如图，∠C=∠EDB，∠2=∠3，求证：∠B=∠FDC．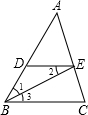
如图所示，已知BE平分∠ABC，∠1=∠2，求证：∠AED=∠C．完善以下推理过程．
4．计算（-xy2）3的结果是（ ）
| A． | x3y6 | B． | -x3y6 | C． | -x4y5 | D． | x4y5 |