我们知道.在反比例函数y=$\frac{2}{x}$的图象上任取一点.过该点分别向两条坐标轴画垂线.这两条垂线与坐标轴围成的矩形面积始终是2．如果在某个函数的图象上任取一点.按同样的方式得到的矩形的周长始终是2.这个函数是y=-x+1．(写出一个满足条件的函数表达式及自变量的取值范围) 题目和参考答案——青夏教育精英家教网——

题目内容

20．我们知道，在反比例函数y=$\frac{2}{x}$的图象上任取一点，过该点分别向两条坐标轴画垂线，这两条垂线与坐标轴围成的矩形面积始终是2．如果在某个函数的图象上任取一点，按同样的方式得到的矩形的周长始终是2，这个函数是y=-x+1（0＜x＜1）．（写出一个满足条件的函数表达式及自变量的取值范围）

分析根据矩形的周长公式进行列式计算．

解答解：答案不唯一，如y=-x+1（0＜x＜1），y=-x-1（-1＜x＜0），y=x+1（-1＜x＜0），y=x-1（0＜x＜1）．
故答案可以是：如y=-x+1（0＜x＜1）．

点评本题考查了一次函数图象上点的坐标特征和反比例函数系数k的几何意义．解题时需要掌握矩形的周长的计算方法．

练习册系列答案

综合复习与测试系列答案

课时总动员系列答案

期末赢家系列答案

天天向上提分金卷系列答案

新思路辅导与训练系列答案

说明与检测系列答案

全程优选测试卷系列答案

沸腾英语系列答案

考点同步解读系列答案

同步导学创新学习系列答案

相关题目

10．已知不等式4x-a≤0的正整数解是1，2，则a的取值范围是（　　）

11．关于x的一元二次方程（a-1）x²-2x+3=0没有实数根，则整数a的最小值是（　　）

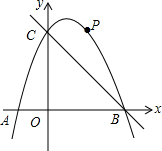如图，在平面直角坐标系中，二次函数y=-x²+bx+c的图象与x轴交于A、B两点，与y轴交于C（0，3），A点在原点的左侧，B点的坐标为（3，0）．点P是抛物线上一个动点，且在直线BC的上方．
（1）求这个二次函数的表达式．
（2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
（3）当点P运动到什么位置时，四边形 ABPC的面积最大，并求出此时点P的坐标和四边形ABPC的最大面积．

15．如图①，在等边△ABC中，CD⊥AB，垂足为D，⊙O的圆心与点D重合，⊙O与线段CD交于点E，且CE=4cm．将⊙O沿DC方向向上平移1cm后，如图②，⊙O恰与△ABC的边AC、BC相切，则等边△ABC的边长为$\frac{14\sqrt{3}}{3}$cm．

5．剪纸是我国最古老的民间艺术之一，被列入第四批人类非物质遗传代表作名录，下列剪纸作品中，既是中心对称图形又是轴对称图形的是（　　）

12．计算：
（1）$\sqrt{0.04}+\root{3}{-64}-\sqrt{\frac{1}{4}}$
（2）|1-$\sqrt{2}$|+|$\sqrt{2}-\sqrt{3}$|+|$\sqrt{3}-2$|

9．在平面直角坐标系xOy中，直线y=k₁x+b与x轴交于点B，与y轴交于点C，与反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限交于点A（3，1），连接OA．
（1）求反比例函数y=$\frac{{k}_{2}}{x}$的解析式；
（2）若S_△AOB：S_△BOC=1：2，求直线y=k₁x+b的解析式．

10．有一箱子装有3张分别标示4，5，6的号码牌，已知小明以每次取一张且取后不放回的方式，先后取出2张牌，组成一个二位数，则组成的二位数是6的倍数的概率是（　　）