题目内容
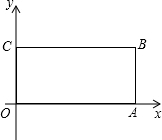 如图,在直角坐标系中,点B(4,2),过点分别作BA⊥x轴于A,BC⊥y轴于C,直线l经过点O并将四边形OABC分为两部分,它们的面积之比为1:2.
如图,在直角坐标系中,点B(4,2),过点分别作BA⊥x轴于A,BC⊥y轴于C,直线l经过点O并将四边形OABC分为两部分,它们的面积之比为1:2.(1)直接写出点A的坐标;
(2)求直线l的解析式.
考点:矩形的性质,待定系数法求一次函数解析式
专题:
分析:(1)根据矩形的性质,结合B点坐标可得A(4,0);
(2)首先根据面积比求出D点坐标,再设出正比例函数,代入D点坐标可得函数解析式.
(2)首先根据面积比求出D点坐标,再设出正比例函数,代入D点坐标可得函数解析式.
解答: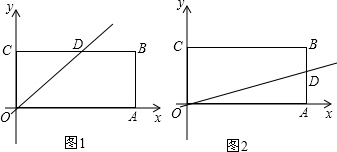 解:(1)∵点B(4,2),
解:(1)∵点B(4,2),
∴A(4,0);
(2)∵点B(4,2),
∴矩形ABCD的面积为4×2=8,
如图1,∵直线l经过点O并将四边形OABC分为两部分,它们的面积之比为1:2.
∴△COD的面积:8×
=
,
∵CO=2,
∴
×2•CD=
,
∴CD=
,
∴D(
,2),
设直线l的解析式为y=kx,则2=
k,
解得k=
,
故直线l的解析式为y=
x;
如图2,∵直线l经过点O并将四边形OABC分为两部分,它们的面积之比为1:2.
∴△AOD的面积:8×
=
,
∵AO=4,
∴D(4,
),
设直线l的解析式为y=kx,
∴
=4k,
k=
,
∴直线l的解析式为y=
x.
 解:(1)∵点B(4,2),
解:(1)∵点B(4,2),∴A(4,0);
(2)∵点B(4,2),
∴矩形ABCD的面积为4×2=8,
如图1,∵直线l经过点O并将四边形OABC分为两部分,它们的面积之比为1:2.
∴△COD的面积:8×
| 1 |
| 3 |
| 8 |
| 3 |
∵CO=2,
∴
| 1 |
| 2 |
| 8 |
| 3 |
∴CD=
| 8 |
| 3 |
∴D(
| 8 |
| 3 |
设直线l的解析式为y=kx,则2=
| 8 |
| 3 |
解得k=
| 3 |
| 4 |
故直线l的解析式为y=
| 3 |
| 4 |
如图2,∵直线l经过点O并将四边形OABC分为两部分,它们的面积之比为1:2.
∴△AOD的面积:8×
| 1 |
| 3 |
| 8 |
| 3 |
∵AO=4,
∴D(4,
| 8 |
| 3 |
设直线l的解析式为y=kx,
∴
| 8 |
| 3 |
k=
| 2 |
| 3 |
∴直线l的解析式为y=
| 2 |
| 3 |
点评:此题主要考查了矩形的性质,以及正比例函数的应用,关键是掌握矩形对边平行且相等.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目

 如图,长阳公园有四棵树,A、B、C、D(单位:米).
如图,长阳公园有四棵树,A、B、C、D(单位:米).
 阅读:
阅读: 如图,四边形ABCD中,∠DAB=90°,AB=3,AD=4,BC=12,CD=13,求四边形ABCD的面积.
如图,四边形ABCD中,∠DAB=90°,AB=3,AD=4,BC=12,CD=13,求四边形ABCD的面积.