题目内容
 如图,四边形ABCD中,∠DAB=90°,AB=3,AD=4,BC=12,CD=13,求四边形ABCD的面积.
如图,四边形ABCD中,∠DAB=90°,AB=3,AD=4,BC=12,CD=13,求四边形ABCD的面积.考点:勾股定理,勾股定理的逆定理
专题:
分析:连接BD,先根据勾股定理求出BD的长度,再根据勾股定理的逆定理判断出△BCD的形状,再利用三角形的面积公式求解即可.
解答: 解:连接BD,
解:连接BD,
∵∠DAB=90°,AB=3,AD=4,
∴BD=
=5,
∵52+122=132,
∴∠DBC=90°,
∴四边形ABCD的面积=
×5×12-
×3×4=24.
 解:连接BD,
解:连接BD,∵∠DAB=90°,AB=3,AD=4,
∴BD=
| AB2+AD2 |
∵52+122=132,
∴∠DBC=90°,
∴四边形ABCD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是勾股定理,勾股定理的逆定理及三角形的面积,能根据勾股定理的逆定理判断出△BCD的形状是解答此题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目

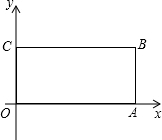 如图,在直角坐标系中,点B(4,2),过点分别作BA⊥x轴于A,BC⊥y轴于C,直线l经过点O并将四边形OABC分为两部分,它们的面积之比为1:2.
如图,在直角坐标系中,点B(4,2),过点分别作BA⊥x轴于A,BC⊥y轴于C,直线l经过点O并将四边形OABC分为两部分,它们的面积之比为1:2. 两个大小不同的等边△ABC和等边△DEC如图摆放,连接AE、BD,M、N、P、Q分别为线段AB、BD、ED、AE的中点.
两个大小不同的等边△ABC和等边△DEC如图摆放,连接AE、BD,M、N、P、Q分别为线段AB、BD、ED、AE的中点.