题目内容
4．某人随意投掷一枚均匀的骰子，投掷了n次，其中有m次掷出的点数是偶数，即掷出的点数是偶数的频率为$\frac{m}{n}$，则下列说法正确的是（ ）| A． | $\frac{m}{n}$一定等于$\frac{1}{2}$ | |
| B． | $\frac{m}{n}$一定不等于$\frac{1}{2}$ | |
| C． | $\frac{m}{n}$一定大于$\frac{1}{2}$ | |
| D． | 投掷的次数很多时，$\frac{m}{n}$稳定在$\frac{1}{2}$附近 |
分析 根据在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近判断即可．
解答 解：某人随意投掷一枚均匀的骰子，投掷了n次，其中有m次掷出的点数是偶数，即掷出的点数是偶数的频率为$\frac{m}{n}$，
则投掷的次数很多时，$\frac{m}{n}$稳定在$\frac{1}{2}$附近，
故选D
点评 此题考查了利用频率估计概率，解题的关键是理解“在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近”．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
相关题目
7．
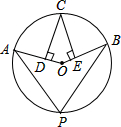如图，点A，B，C，P在⊙O上，CD⊥OA，CE⊥OB，垂足分别为D，E，∠DCE=40°，则∠P的度数为（ ）
如图，点A，B，C，P在⊙O上，CD⊥OA，CE⊥OB，垂足分别为D，E，∠DCE=40°，则∠P的度数为（ ）| A． | 140° | B． | 70° | C． | 60° | D． | 40° |
15．下列方程的变形中，正确的是（ ）
| A． | 由$-\frac{1}{3}$x=0，得x=3 | B． | 由6y=3，得y=2 | ||
| C． | 由x-5=-3，得x=5+3 | D． | 由2=x-4，得x=4+2 |
19．
如图，在△ABC中，∠ACB=90°，∠A=30°，AB的垂直平分线分别交AB和AC于点D，E，AE=2，CE=（ ）
如图，在△ABC中，∠ACB=90°，∠A=30°，AB的垂直平分线分别交AB和AC于点D，E，AE=2，CE=（ ）| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\sqrt{5}$ |
9．暑假期间，读大学的王刚同学回家帮助父母开了一家冷饮销售摊点，他发现销售某种冷饮每天的成本C（元）与销售数量t（个）可以近似地表示为C=3t+100，为了每天获取最大利润，他经过调查，得到销售数量t与销售单价x之间有如下关系：
（1）试用已学过的函数刻画销售数量t与销售单价x之间的关系；
（2）试求每天的利润P（元）与销售单价x的函数关系；（每天利润=销售单价×销售数量-每天成本）
（3）王刚的弟弟认为“定价越高获利越多”，你同意他的观点吗？请求出每天的最大利润．
| 销售单价x/元 | 4 | 5 | 6 | 7 | 8 |
| 销售数量t/件 | 120 | 100 | 80 | 60 | 40 |
（2）试求每天的利润P（元）与销售单价x的函数关系；（每天利润=销售单价×销售数量-每天成本）
（3）王刚的弟弟认为“定价越高获利越多”，你同意他的观点吗？请求出每天的最大利润．