题目内容
19. 如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E,AE=2,CE=( )
如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E,AE=2,CE=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
分析 由AB的垂直平分线DE交AC于点D,垂足为E,根据线段垂直平分线的性质,可求得BE=AE=2,由BE=AE,∠A=30°,即可求得∠C的度数,继而可得∠CBE,根据含30°角的直角三角形的性质即可求得答案.
解答  解:∵DE是AB的垂直平分线,
解:∵DE是AB的垂直平分线,
∴BE=AE=2,∠ABE=∠A=30°,
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∴∠CBE=30°,
∴CE=$\frac{1}{2}$BE=1,
故选A.
点评 此题考查了线段垂直平分线的性质、30°角的直角三角形的性质以及等腰三角形的性质,熟练掌握30°角的直角三角形的性质是解决问题的关键.

练习册系列答案
相关题目
2.据《南国早报》报道:2016年广西高考报名人数约为332000人,创历史新高,其中数据332000用科学记数法表示为( )
| A. | 0.332×106 | B. | 3.32×105 | C. | 3.32×104 | D. | 33.2×104 |
7.下列定理中,没有逆定理的是( )
| A. | 直角三角形的两锐角互余 | |
| B. | 同位角相等,两直线平行 | |
| C. | 对顶角相等 | |
| D. | 直角三角形两直角边平方和等于斜边的平方 |
14.把x2+x+m因式分解得(x-1)(x+2),则m的值为( )
| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
4.某人随意投掷一枚均匀的骰子,投掷了n次,其中有m次掷出的点数是偶数,即掷出的点数是偶数的频率为$\frac{m}{n}$,则下列说法正确的是( )
| A. | $\frac{m}{n}$一定等于$\frac{1}{2}$ | |
| B. | $\frac{m}{n}$一定不等于$\frac{1}{2}$ | |
| C. | $\frac{m}{n}$一定大于$\frac{1}{2}$ | |
| D. | 投掷的次数很多时,$\frac{m}{n}$稳定在$\frac{1}{2}$附近 |
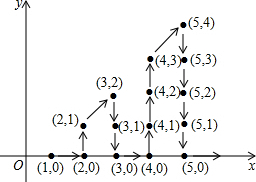 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)根据这个规律探索可得,第2016个点的横坐标为63.
如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)根据这个规律探索可得,第2016个点的横坐标为63.