题目内容
12.某文化用品店用1975元购进一批学生书包,面市后发现供不应求,该店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果购进第二批用了6225元.(1)求第一批书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是118元,则全部售出后,商店共盈利多少元?
分析 (1)本题的关键描述语是:“数量是第一批购进数量的3倍”;等量关系为:用6225元购进学生书包的数量=用1975元购进学生书包的数量×3.
(2)根据盈利=总售价-总进价列式计算即可.
解答 解:(1)设第一批书包的单价是x元,则第二批书包的单价是(x+4)元.
由题意得:$\frac{6225}{x+4}$=$\frac{1975}{x}$×3.
解得:x=79.
经检验:x=79是原方程的根.
答:第一批书包的单价是79元.
(2)$\frac{1975}{79}$×(118-79)+$\frac{6225}{83}$×(118-83)=3600(元).
答:商店共盈利3600元.
点评 本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
7.下列定理中,没有逆定理的是( )
| A. | 直角三角形的两锐角互余 | |
| B. | 同位角相等,两直线平行 | |
| C. | 对顶角相等 | |
| D. | 直角三角形两直角边平方和等于斜边的平方 |
4.某人随意投掷一枚均匀的骰子,投掷了n次,其中有m次掷出的点数是偶数,即掷出的点数是偶数的频率为$\frac{m}{n}$,则下列说法正确的是( )
| A. | $\frac{m}{n}$一定等于$\frac{1}{2}$ | |
| B. | $\frac{m}{n}$一定不等于$\frac{1}{2}$ | |
| C. | $\frac{m}{n}$一定大于$\frac{1}{2}$ | |
| D. | 投掷的次数很多时,$\frac{m}{n}$稳定在$\frac{1}{2}$附近 |
2.菱形的周长为20cm,两个相邻的内角的度数之比为1:2,则较长的对角线的长度是( )
| A. | 20$\sqrt{3}$ | B. | 5$\sqrt{3}$cm | C. | $\frac{5}{2}$$\sqrt{3}$cm | D. | 5cm |

 如图,△ABC中,∠C=90°,AC=3,BC=4,AB的垂直平分线交AB于E,交BC于D,求BD的长.
如图,△ABC中,∠C=90°,AC=3,BC=4,AB的垂直平分线交AB于E,交BC于D,求BD的长.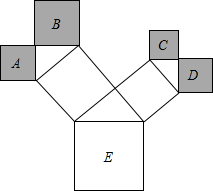 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别是4、6、3、4,则最大正方形E的面积是17.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别是4、6、3、4,则最大正方形E的面积是17.