题目内容
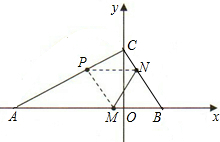如图，已知A（-3，0），C（0，| 3 |
| 1 |
| 3 |
（1）求出∠ABC的度数；
（2）若点M、N同时从B点出发，均以每秒1个单位长度的速度分别沿BA、BC边运动，其中一个点到达终点时，另一个点也随之停止运动，当运动时间为t秒时，连结MN，将△BMN沿MN翻折，B点恰好落在AC边上的P处，求t的值；
（3）在（2）的情况下，直接写出点P的坐标．
考点：相似形综合题
专题：
分析：（1）根据A（-3，0），C（0，
），OB=
OA，利用三角函数即可得到答案．
（2）由（1）可以断定三角形MNB的形状，再利用三角形相似的性质，得出比例线段得到答案．
（3）t的值确定，P点的坐标即可得到．
| 3 |
| 1 |
| 3 |
（2）由（1）可以断定三角形MNB的形状，再利用三角形相似的性质，得出比例线段得到答案．
（3）t的值确定，P点的坐标即可得到．
解答：解：（1）∵A（-3，0），C（0，
），
∴OA=3，OC=
点B在x轴正半轴上，且OB=
OA．
∴OB=1．
∴tan∠ABC=
=
，
∴∠ABC=60°．
（2）∵BM=BN=PM=PN=t，
∴四边形BMPN是菱形，
∴PM∥BC，
∴△APM∽△ABC，
∴
=
，
又∵OA=3，OC=
，OB=1，
根据勾股定理得：BC=2，
∴有
=
解之得：t=
．
（3）过点P作PD⊥AB，垂足为D，
因为t=
，所以BM=PM=
，
∠PMD=∠CBA=60°，
所以PD=
，DM=
，
∴OD=1，
∴P点的坐标是(-1，
)．
| 3 |
∴OA=3，OC=
| 3 |
点B在x轴正半轴上，且OB=
| 1 |
| 3 |
∴OB=1．
∴tan∠ABC=
| CO |
| BO |
| 3 |
∴∠ABC=60°．
（2）∵BM=BN=PM=PN=t，
∴四边形BMPN是菱形，
∴PM∥BC，
∴△APM∽△ABC，
∴
| AM |
| AB |
| PM |
| BC |
又∵OA=3，OC=
| 3 |
根据勾股定理得：BC=2，
∴有
| 4-t |
| 4 |
| t |
| 2 |
解之得：t=
| 4 |
| 3 |
（3）过点P作PD⊥AB，垂足为D，
因为t=
| 4 |
| 3 |
| 4 |
| 3 |
∠PMD=∠CBA=60°，
所以PD=
2
| ||
| 3 |
| 2 |
| 3 |
∴OD=1，
∴P点的坐标是(-1，
2
| ||
| 3 |
点评：本题考查了三角函数的计算以及相似三角形的判定与性质的简单应用，解答本题的关键是要学会作辅助线．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
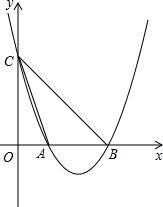如图，已知抛物线y=ax2+bx+c经过A（2，0），B（6，0），C（0，6），其对称轴交x轴于M点，
