题目内容
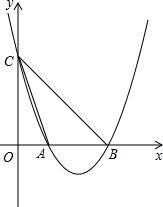 如图,已知抛物线y=ax2+bx+c经过A(2,0),B(6,0),C(0,6),其对称轴交x轴于M点,
如图,已知抛物线y=ax2+bx+c经过A(2,0),B(6,0),C(0,6),其对称轴交x轴于M点,(1)求抛物线的解析式;
(2)已知点P是抛物线上一点,且满足 S△ACP=S△ABP,求P点坐标;
(3)抛物线对称轴是否存在点Q,使△BCQ与△AOC相似?若存在,求出Q点坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:综合题
分析:(1)将三点代入抛物线,利用待定系数法可确定抛物线解析式;
(2)分两种情况讨论,①点P在第四象限,②点P在第一象限,再由S△ACP=S△ABP,y与x的函数关系式,结合抛物线解析式可得x、y的值,也可利用作平行线的方法求解;
(3)在本题的求解过程中,可先将△BCQ与△AOC相似,利用对应边成比例求Q的坐标.
(2)分两种情况讨论,①点P在第四象限,②点P在第一象限,再由S△ACP=S△ABP,y与x的函数关系式,结合抛物线解析式可得x、y的值,也可利用作平行线的方法求解;
(3)在本题的求解过程中,可先将△BCQ与△AOC相似,利用对应边成比例求Q的坐标.
解答: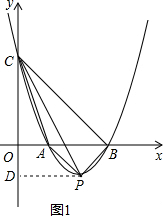 解:(1)将A(2,0),B(6,0),C(0,6),代入抛物线y=ax2+bx+c得:
解:(1)将A(2,0),B(6,0),C(0,6),代入抛物线y=ax2+bx+c得:
,
解得:
∴抛物线的解析式为:y=
x2-4x+6;
(2)方法一:
如图1,P在第四象限时,过P点作PD⊥y轴于D,设P(x,y),
由S△CDP-S△COA-S梯形AODP=S△ABP得,
x(6-y)-
(-y)(2+x)-6=-2y,
∴y=-x+2,
∴-x+2=
x2-4x+6,
解得:x=4或x=2(舍去),
∴P(4,-2)
同理,当P在第一象限时,P(12,30)
∴P1(4,-2),P2(12,30);
方法二:P在第四象限时,过A点作AP∥BC交抛物线于P点,
易得P(4,-2)
P在第一象限时,取BC中点E,作直线AE交抛物线于P,
易得P(12,30),
∴P1(4,-2),P2(12,30);
(3)如图2,过B点作BQ⊥BC,交抛物线对称轴于Q点,
∵OB=OC,∠BOC=90°,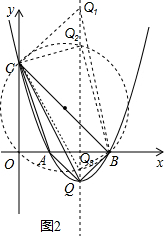
∴∠CBO=45°=∠QBO,
∴BM=MQ=2,
计算可得BC=6
,BQ=2
,
在△AOC与△QBC中,
∵
=
=
,
∠AOC=90°=∠QBC,
∴△AOC∽△QBC,
由
x2-4x+6=-2,
解得x1=x2=4,
∴Q((4,-2),
同理,过C作CQ1⊥BC交MQ于Q1,可验证△AOC与△QBC的边不对应成比例,
故Q1不满足条件;
以BC为直径作圆交MQ于Q2,Q3,经验证均不满足条件,
∴存在唯一满足条件的Q点,Q((4,-2).
 解:(1)将A(2,0),B(6,0),C(0,6),代入抛物线y=ax2+bx+c得:
解:(1)将A(2,0),B(6,0),C(0,6),代入抛物线y=ax2+bx+c得:
|
解得:
|
∴抛物线的解析式为:y=
| 1 |
| 2 |
(2)方法一:
如图1,P在第四象限时,过P点作PD⊥y轴于D,设P(x,y),
由S△CDP-S△COA-S梯形AODP=S△ABP得,
| 1 |
| 2 |
| 1 |
| 2 |
∴y=-x+2,
∴-x+2=
| 1 |
| 2 |
解得:x=4或x=2(舍去),
∴P(4,-2)
同理,当P在第一象限时,P(12,30)
∴P1(4,-2),P2(12,30);
方法二:P在第四象限时,过A点作AP∥BC交抛物线于P点,
易得P(4,-2)
P在第一象限时,取BC中点E,作直线AE交抛物线于P,
易得P(12,30),
∴P1(4,-2),P2(12,30);
(3)如图2,过B点作BQ⊥BC,交抛物线对称轴于Q点,
∵OB=OC,∠BOC=90°,

∴∠CBO=45°=∠QBO,
∴BM=MQ=2,
计算可得BC=6
| 2 |
| 2 |
在△AOC与△QBC中,
∵
| OC |
| BC |
| 1 | ||
|
| OA |
| BQ |
∠AOC=90°=∠QBC,
∴△AOC∽△QBC,
由
| 1 |
| 2 |
解得x1=x2=4,
∴Q((4,-2),
同理,过C作CQ1⊥BC交MQ于Q1,可验证△AOC与△QBC的边不对应成比例,
故Q1不满足条件;
以BC为直径作圆交MQ于Q2,Q3,经验证均不满足条件,
∴存在唯一满足条件的Q点,Q((4,-2).
点评:本题考查了二次函数的综合,涉及了待定系数法求二次函数解析式、三角形的面积、相似三角形的相似与性质,综合性较强,难度较大,解答此类题目关键是数形结合、分类讨论思想的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
比较三个数-3,-π,-
的大小,下列结论正确的是( )
| 10 |
A、-π>-3>-
| ||
B、-
| ||
C、-
| ||
D、-3>-π>-
|
 如图,在△ABC中,DE∥BC,
如图,在△ABC中,DE∥BC,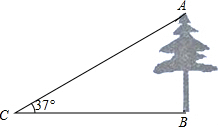 如图,在一次数学课外实践活动,小文在点C处测得树的顶端A的仰角为37°,BC=20m,求树的高度AB.
如图,在一次数学课外实践活动,小文在点C处测得树的顶端A的仰角为37°,BC=20m,求树的高度AB.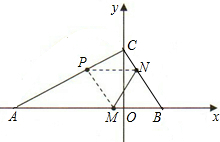 如图,已知A(-3,0),C(0,
如图,已知A(-3,0),C(0,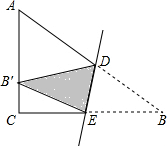 在Rt△ABC中,∠C=90°,AC=6,BC=8,将△BDC沿直线DE折叠,使B落在AC的三等分点B′处,求CE的长.
在Rt△ABC中,∠C=90°,AC=6,BC=8,将△BDC沿直线DE折叠,使B落在AC的三等分点B′处,求CE的长.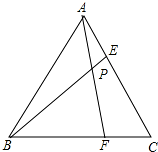 等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.
等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.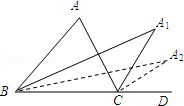 如图,在△ABC中,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…∠A2013BC与∠A2013CD的平分线相交于点A2014,得∠A2014,根据题意填空:
如图,在△ABC中,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…∠A2013BC与∠A2013CD的平分线相交于点A2014,得∠A2014,根据题意填空: