题目内容
设函数y=
与y=x-2的图象的交点坐标为(a,b),则a2+b2的值为 .
| 1 |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:根据函数解析式,可的方程组,根据解方程组,可得交点坐标,根据代数式求值,可得答案.
解答:解;由函数y=
与y=x-2的图象的交点,得
,解得
,或
,
a2+b2=x2+y2=(1+
)2+(
-1)2=1+2+2
+1+2-2
=6,
a2+b2=x2+y2=(1-
)2+(-
-1)2=1-2
+2+1+2
+2=6,
故答案为:6.
| 1 |
| x |
|
|
|
a2+b2=x2+y2=(1+
| 2 |
| 2 |
| 2 |
| 2 |
a2+b2=x2+y2=(1-
| 2 |
| 2 |
| 2 |
| 2 |
故答案为:6.
点评:本题考查了反比例函数一次函数的交点问题,先解方程组,再求代数式的值.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 已知:如图,反比例函数y=
已知:如图,反比例函数y= 如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.
如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.
 如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=
如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3= 如图,在△ABC中,DE∥BC,
如图,在△ABC中,DE∥BC, 李老师开车从甲地到相距240千米的乙地,如果邮箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图所示,那么到达乙地时邮箱剩余油量是
李老师开车从甲地到相距240千米的乙地,如果邮箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图所示,那么到达乙地时邮箱剩余油量是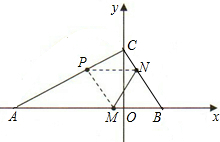 如图,已知A(-3,0),C(0,
如图,已知A(-3,0),C(0,