题目内容
15．
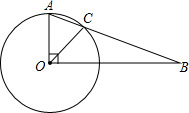如图，在⊙O中，半径OA⊥OB，∠B=28°，求∠BOC的度数．
分析 先根据垂直定义得到∠AOB=90°，再根据互余计算出∠A=62°，利用半径相等得到∠ACO=∠A=62°，然后根据三角形外角性质求∠BOC的度数．
解答 解：∵OA⊥OB，
∴∠AOB=90°，
∴∠A=90°-∠B=90°-28°=62°，
∵OA=OC，
∴∠ACO=∠A=62°，
而∠ACO=∠BOC+∠B，
∴∠BOC=62°-28°=34°．
点评 本题考查了圆的认识：圆可以看做是所有到定点O的距离等于定长r的点的集合，掌握与圆有关的概念（弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等）．
练习册系列答案
相关题目
如图，方格纸中△ABC的3个顶点分别在小正方形的顶点（格点）上，这样的三角形叫格点三角形，图中与△ABC全等的格点三角形共有15个（不含△ABC）．
5．
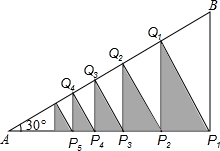如图，在Rt△ABP1中，∠AP1B=Rt∠，∠A=30°，BP1=2，过点P1作P1Q1⊥AB，垂足Q1，过点Q1作Q1P2⊥AP1，垂足P2，过点P2作P2Q2⊥AB，垂足Q2，…如此无限下去，得到一系列阴影三角形△P1Q1P2、△P2Q2P3、△P3Q3P4…，则所有这些阴影三角形的面积和是（ ）
如图，在Rt△ABP1中，∠AP1B=Rt∠，∠A=30°，BP1=2，过点P1作P1Q1⊥AB，垂足Q1，过点Q1作Q1P2⊥AP1，垂足P2，过点P2作P2Q2⊥AB，垂足Q2，…如此无限下去，得到一系列阴影三角形△P1Q1P2、△P2Q2P3、△P3Q3P4…，则所有这些阴影三角形的面积和是（ ）| A． | $\sqrt{3}$ | B． | $\frac{3}{4}\sqrt{3}$ | C． | $\frac{6}{7}\sqrt{3}$ | D． | 不能确定 |
如图，△ABC是等边三角形，CE是外角平分线，点D在AC上，连接BD并延长与CE交于点E．