题目内容
6. 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长与CE交于点E.(1)求证:△ABD∽△CED;
(2)若AB=10,AD=2CD,求CE的长.
分析 (1)由于△ABC是等边三角形,易知∠A=60°,∠ACF=120°;而CE平分∠ACF,可得∠A=∠DCE=60°,又已知了一组对顶角,两组对应角相等,可判定所求的两个三角形相似;
(2)由相似三角形的对应边成比例,即可求得CE的长.
解答 (1)证明:∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,∠ACF=120°;
∵CE是外角平分线,
∴∠ACE=60°;
∴∠BAC=∠ACE;
又∵∠ADB=∠CDE,
∴△ABD∽△CED;
(2)解:∵△ABD∽△CED,
∴$\frac{AB}{CE}=\frac{AD}{CD}$,
∵AD=2DC,
∴AB=2CE,
∴CE=$\frac{1}{2}$AB=5.
点评 此题考查了相似三角形的判定与性质与等边三角形的性质,以及角平分线的定义.注意掌握有两角对应相等的三角形相似与相似三角形的对应边成比例是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.一次函数的一般形式是(k、b是常数)( )
| A. | y=kx+b | B. | y=kx | C. | y=kx+b(k≠0) | D. | y=x |
11.若抛物线y=a(x-2)2+a2+a顶点在x轴上,则a的值为( )
| A. | -1 | B. | 0 | C. | 0或-1 | D. | 任意实数 |
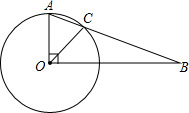 如图,在⊙O中,半径OA⊥OB,∠B=28°,求∠BOC的度数.
如图,在⊙O中,半径OA⊥OB,∠B=28°,求∠BOC的度数.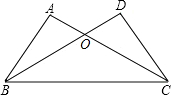 如图,AC与BD交于O点,若AB=DC,请补充一个条件:AC=BD(或∠ABC=∠DCB等),使△ABC≌△DCB.
如图,AC与BD交于O点,若AB=DC,请补充一个条件:AC=BD(或∠ABC=∠DCB等),使△ABC≌△DCB.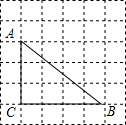 如图,正方形网格的每一个小正方形的边长都为1,△ABC的三个顶点都在正方形的顶点上,完成下面问题:
如图,正方形网格的每一个小正方形的边长都为1,△ABC的三个顶点都在正方形的顶点上,完成下面问题: