题目内容
如图：正方形ABCD的一条对角线AC的长为4cm，求它的边长和面积．（长度精确到0.1cm）考点：勾股定理,正方形的性质
专题：
分析：由正方形的性质知：△ABC是等腰直角三角形，已知了斜边AC的长，即可求得直角边AB、BC的值，也就求得了正方形的边长，进而可求出其面积
解答：解：∵四边形ABCD为正方形，
∴AB=BC，∠ABC=90°，
故AC=
AB，
即AB=2
≈2.8cm，
故正方形的面积S=a2=8cm2，
答：正方形的边长为2.8cm，面积为8cm2．
∴AB=BC，∠ABC=90°，
故AC=
| 2 |
即AB=2
| 2 |
故正方形的面积S=a2=8cm2，
答：正方形的边长为2.8cm，面积为8cm2．
点评：本题考查了勾股定理的运用以及正方形的性质，解题的关键是将图形转化到等腰直角三角形中求解．对正方形的性质需有充分认识．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
某股民用30000元买进甲、乙两种股票，在甲股票下跌10%，乙股票升值8%时全部卖出，赚得1500元（含税），则该股民原来购买的甲、乙两种股票所用钱数的比例为（ ）
| A、2：3 | B、3：2 |
| C、1：5 | D、5：1 |
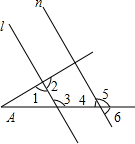图中直线l、n分别截∠A的两边，且l∥n，∠3=∠1+∠4．根据图中标示的角，判断下列各角的度数关系中正确的是（ ）| A、∠2+∠5＞180° |
| B、∠2+∠3＜180° |
| C、∠1+∠6＞180° |
| D、∠3+∠4＜180° |
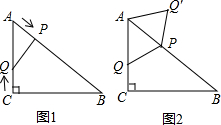如图1，Rt△ABC中，AC=6cm，BC=8cm，点P以2cm/s的速度从A处沿AB方向匀速运动，点Q以1cm/s的速度从C处沿CA方向匀速运动．连接PQ，若设运动的时间为t（s）（0＜t＜5）．解答下列问题：