题目内容
如图，已知△ABC中，AB=AC=12厘米，∠B=∠C，BC=8厘米，点D为AB的中点．如果点P在线段BC上以2厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．若点Q的运动速度为v厘米/秒，则当△BPD与△CQP全等时，v的值为（ ）| A、2 | B、3 | C、2或3 | D、1或5 |
考点：全等三角形的判定
专题：动点型
分析：已知∠B=∠C，根据全等三角形的性质得出BD=PC，或BP=PC，进而算出时间t，再算出v即可．
解答：解：设经过t秒后，△BPD与△CQP全等，
∵AB=AC=12厘米，点D为AB的中点，
∴BD=6厘米，
∵∠B=∠C，BP=CQ=2t，
∴要使△BPD和△CQP全等，只有BD=CP=6厘米，
则8-6=2t，
解得：t=1，
v=2÷1=2厘米/秒，
当BP=PC时，
∵BC=8cm，
∴PB=4cm，
t=4÷2=2s，
QC=BD=6cm，
v=6÷2=3厘米/秒．
故选：C．
∵AB=AC=12厘米，点D为AB的中点，
∴BD=6厘米，
∵∠B=∠C，BP=CQ=2t，
∴要使△BPD和△CQP全等，只有BD=CP=6厘米，
则8-6=2t，
解得：t=1，
v=2÷1=2厘米/秒，
当BP=PC时，
∵BC=8cm，
∴PB=4cm，
t=4÷2=2s，
QC=BD=6cm，
v=6÷2=3厘米/秒．
故选：C．
点评：本题考查了等腰三角形的性质和全等三角形的性质，注意：全等三角形的对应边相等．
练习册系列答案
相关题目
如图，∠DCA=∠ECB，CD=CA，若使△ABC≌△DEC，则下列添加的条件错误的是（ ）| A、CB=CE |
| B、∠B=∠E |
| C、∠A=∠D |
| D、AB=DE |
为了了解某校七年级260名男生的身高情况，从中随机抽查了30名男生，对他们的身高进行统计分析，发现这
30名男生身高的平均数是160cm，下列结论中不正确是（ ）
30名男生身高的平均数是160cm，下列结论中不正确是（ ）
| A、260名男生的身高是总体 |
| B、抽取的30名男生的身高是总体的一个样本 |
| C、估计这260名男生身高的平均数一定是160cm |
| D、样本容量是30 |
一位运动鞋经销商到一所学校抽样调查了10名男生的鞋号，其号码分别为：37，38，39，40，41，41，41，42，43，45，经销商最感兴趣的是这组数据中的（ ）
| A、平均数 | B、中位数 |
| C、众数 | D、方差 |
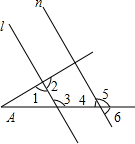图中直线l、n分别截∠A的两边，且l∥n，∠3=∠1+∠4．根据图中标示的角，判断下列各角的度数关系中正确的是（ ）| A、∠2+∠5＞180° |
| B、∠2+∠3＜180° |
| C、∠1+∠6＞180° |
| D、∠3+∠4＜180° |
