题目内容
13．$\sqrt{81}$的平方根是±3，（-6）2的算术平方根是6．分析 先求得$\sqrt{81}$、（-6）2的值，然后依据平方根和算术平方根的定义求解即可．
解答 解：$\sqrt{81}$=9，9的平方根是±3，（-6）2=36，36的算术方根是6．
故答案为：±3；6．
点评 本题主要考查的是算术平方根、平方根的定义，求得$\sqrt{81}$、（-6）2的值是解题的关键．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
3．
我们曾经通过列表、画图象，研究了函数y=ax2（a≠0）的性质，知道它的图象是一条抛物线，通过图象还研究了它的相关性质；经过平移函数y=ax2（a≠0）的图象还可得到函数y=a（x-h）2+k，（a≠0）的图象．用类似的方法还可研究其他函数的有关性质．
下面请你通过类比，尝试研究一下函数y=$\frac{1}{2}$x3的性质：
（1）完成下表：
（2）在所给坐标系中作出函数y=$\frac{1}{2}$x3的图象；
（3）观察你画的函数y=$\frac{1}{2}$x3的图象，回答下列问题：
①函数y=$\frac{1}{2}$x3图象的对称性下列说法正确的是C．
A．关于x轴对称 B．关于y轴对称
C．关于原点对称 D．既不是轴对称也不是中心对称
②随x的增大，y有怎样的变化？
③y是否有最大或最小值？
④将函数y=$\frac{1}{2}$x3的图象向左平移一个单位，再向上平移两个单位．可得到怎样的函数表达式，请直接将你的猜想写出来？
我们曾经通过列表、画图象，研究了函数y=ax2（a≠0）的性质，知道它的图象是一条抛物线，通过图象还研究了它的相关性质；经过平移函数y=ax2（a≠0）的图象还可得到函数y=a（x-h）2+k，（a≠0）的图象．用类似的方法还可研究其他函数的有关性质．下面请你通过类比，尝试研究一下函数y=$\frac{1}{2}$x3的性质：
（1）完成下表：
| x | … | -2 | -1 | 0 | 1 | 2 | … | ||
| y | … | 0 | 4 | … |
（3）观察你画的函数y=$\frac{1}{2}$x3的图象，回答下列问题：
①函数y=$\frac{1}{2}$x3图象的对称性下列说法正确的是C．
A．关于x轴对称 B．关于y轴对称
C．关于原点对称 D．既不是轴对称也不是中心对称
②随x的增大，y有怎样的变化？
③y是否有最大或最小值？
④将函数y=$\frac{1}{2}$x3的图象向左平移一个单位，再向上平移两个单位．可得到怎样的函数表达式，请直接将你的猜想写出来？
1．若$\sqrt{{a}^{2}}$=a，则实数a在数轴上的对应点一定在（ ）
| A． | 原点左侧 | B． | 原点右侧 | C． | 原点或原点左侧 | D． | 原点或原点右侧 |
8．下列各式中，正确的是（ ）
| A． | $\sqrt{25}$=±5 | B． | $\sqrt{-（\sqrt{5}）^{2}}$=$\sqrt{5}$ | C． | $\sqrt{16\frac{1}{4}}$=4$\frac{1}{2}$ | D． | $\sqrt{\frac{1}{2}}=\frac{\sqrt{2}}{2}$ |
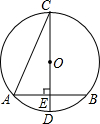如图，已知⊙O的直径CD垂直于弦AB，∠ACD=22.5°，若CD=6cm，则AB的长为3$\sqrt{2}$cm．