题目内容
3. 我们曾经通过列表、画图象,研究了函数y=ax2(a≠0)的性质,知道它的图象是一条抛物线,通过图象还研究了它的相关性质;经过平移函数y=ax2(a≠0)的图象还可得到函数y=a(x-h)2+k,(a≠0)的图象.用类似的方法还可研究其他函数的有关性质.
我们曾经通过列表、画图象,研究了函数y=ax2(a≠0)的性质,知道它的图象是一条抛物线,通过图象还研究了它的相关性质;经过平移函数y=ax2(a≠0)的图象还可得到函数y=a(x-h)2+k,(a≠0)的图象.用类似的方法还可研究其他函数的有关性质.下面请你通过类比,尝试研究一下函数y=$\frac{1}{2}$x3的性质:
(1)完成下表:
| x | … | -2 | -1 | 0 | 1 | 2 | … | ||
| y | … | 0 | 4 | … |
(3)观察你画的函数y=$\frac{1}{2}$x3的图象,回答下列问题:
①函数y=$\frac{1}{2}$x3图象的对称性下列说法正确的是C.
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.既不是轴对称也不是中心对称
②随x的增大,y有怎样的变化?
③y是否有最大或最小值?
④将函数y=$\frac{1}{2}$x3的图象向左平移一个单位,再向上平移两个单位.可得到怎样的函数表达式,请直接将你的猜想写出来?
分析 (1)利用已知函数解析式进而计算得出答案;
(2)利用(1)中所求数据描点连线即可;
(3)①利用函数图象即可得出对称性;
②利用函数图象得出增减性;
③利用函数图象得出有没有最值;
④利用函数平移的性质,左加右减,上加下减即可得出答案.
解答 解:(1)填表如下:
| x | … | -2 | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | 2 | … |
| y | … | -4 | -$\frac{1}{2}$ | -$\frac{1}{16}$ | 0 | $\frac{1}{16}$ | $\frac{1}{2}$ | 4 | … |
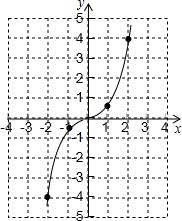
(2)函数$y=\frac{1}{2}{x^3}$的图象如图;
(3)①如图所示:函数y=$\frac{1}{2}$x3图象关于原点对称,
故答案为:C;
②如图所示:y随x的增大而增大;
③如图所示:y既没有最大值也没有最小值;
④将函数$y=\frac{1}{2}{x^3}$的图象向左平移一个单位,再向上平移两个单位可得到:$y=\frac{1}{2}{({x+1})^3}+2$.
点评 此题主要考查了函数问题综合以及函数增减性以及其对称性、最值平移规律等知识,结合已知函数解析式画出图象是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.两个非零有理数的和为正数,那么这两个有理数为( )
| A. | 都是正数 | |
| B. | 至少有一个为正数 | |
| C. | 正数大于负数 | |
| D. | 正数大于负数的绝对值,或都为正数 |
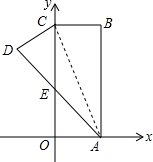 如图,在直角坐标系中,长方形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(2,6),将长方形沿对角线AC翻折,点B落在点D的位置,且AD交y轴于点E,则点D的坐标为(-$\frac{8}{5}$,$\frac{24}{5}$).
如图,在直角坐标系中,长方形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(2,6),将长方形沿对角线AC翻折,点B落在点D的位置,且AD交y轴于点E,则点D的坐标为(-$\frac{8}{5}$,$\frac{24}{5}$).