题目内容
18.如果关于x的不等式组$\left\{\begin{array}{l}{3x-a>0,①}\\{\frac{2x-1}{3}<3②}\end{array}\right.$只有两个整数解,求a的取值范围.分析 先求出每个不等式的解集,再求出不等式组的解集,最后根据已知得出关于a的不等式组,求出即可.
解答 解:$\left\{\begin{array}{l}{3x-a>0①}\\{\frac{2x-1}{3}<3②}\end{array}\right.$
∵解不等式①得:x>$\frac{a}{3}$,
解不等式②得:x<5,
∴不等式组的解集为$\frac{a}{3}$<x<5,
∵不等式组只有两个整数解,
∴2≤$\frac{a}{3}$<3,
解得:6≤a<9,
即a的取值范围为6≤a<9.
点评 本题考查了解一元一次不等式,解一元一次不等式组,不等式组的整数解的应用,解此题的关键是求出关于a的不等式组,难度适中.

练习册系列答案
相关题目
13.为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:
(说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费;
已知小明家2014年4月份用水10吨,交水费30元;5月份用水35吨,交水费150元.
(1)求a、b的值.
(2)实行“阶梯水价”收费之后,该市一户居民用水多少吨时,其当月的平均水费每吨不超过3.3元.
| 用户每月用水量 | 自来水单价(元/吨) | 污水处理费用(元/吨) |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
已知小明家2014年4月份用水10吨,交水费30元;5月份用水35吨,交水费150元.
(1)求a、b的值.
(2)实行“阶梯水价”收费之后,该市一户居民用水多少吨时,其当月的平均水费每吨不超过3.3元.
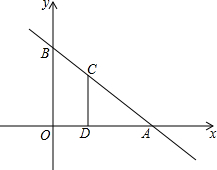 如图,平面直角坐标系中,直线AB:y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A(4,0)、B(0,3)两点,点C为线段AB上的一动点,过点C作CD⊥x轴于D.
如图,平面直角坐标系中,直线AB:y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A(4,0)、B(0,3)两点,点C为线段AB上的一动点,过点C作CD⊥x轴于D. 如图,直线l1是一次函数y=kx+b的图象.
如图,直线l1是一次函数y=kx+b的图象. 如图,在平面直角坐标系中,直线y=-x+6与x轴交于点B,与y轴交于点A,点C是线段AB的中点,求线段OC的长.
如图,在平面直角坐标系中,直线y=-x+6与x轴交于点B,与y轴交于点A,点C是线段AB的中点,求线段OC的长. 如图所示,已知∠1=145°,则∠2=55°.
如图所示,已知∠1=145°,则∠2=55°.