题目内容
9. 如图,直线l1是一次函数y=kx+b的图象.
如图,直线l1是一次函数y=kx+b的图象.(1)求k与b的值;
(2)求与l1平行且过点(3,0)的直线l2的表达式.
分析 (1)根据图象可得一次函数y=kx+b过(0,1),(3,-3)两点,再将这两点的坐标代入得出方程组,解出即可得出k和b的值;
(2)根据直线平行的规律可设直线l2的解析式为y=-$\frac{4}{3}$x+n,将点(3,0)代入利用待定系数法即可求解.
解答 解:(1)根据图象可得一次函数y=kx+b过(0,1),(3,-3)两点,
则$\left\{\begin{array}{l}{b=1}\\{3k+b=-3}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=1}\end{array}\right.$,
(2)∵直线l1的解析式为y=-$\frac{4}{3}$x+1,直线l2与l1平行,
∴可设直线l2的解析式为y=-$\frac{4}{3}$x+n,
将点(3,0)代入,得0=-$\frac{4}{3}$×3+n,解得n=4,
∴直线l2的解析式为y=-$\frac{4}{3}$x+4.
点评 本题考查待定系数法求一次函数解析式,关键是要掌握待定系数法的运用,也考查了两条直线平行的规律.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
14.如果$\frac{1}{{s}_{1}}=\frac{1}{{t}_{1}}+\frac{1}{{t}_{2}}$,$\frac{1}{{s}_{2}}=\frac{1}{{t}_{1}}-\frac{1}{{t}_{2}}$,则$\frac{{s}_{1}}{{s}_{2}}$=( )
| A. | $\frac{{t}_{1}+{t}_{2}}{{t}_{2}-{t}_{1}}$ | B. | $\frac{{t}_{2}-{t}_{1}}{{t}_{2}+{t}_{1}}$ | C. | $\frac{{t}_{1}-{t}_{2}}{{t}_{2}+{t}_{1}}$ | D. | $\frac{{t}_{1}+{t}_{2}}{{t}_{1}-{t}_{2}}$ |
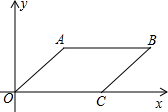 如图,平行四边形ABCO四个顶点的坐标分别为A($\sqrt{3}$,$\sqrt{3}$),B(3$\sqrt{3}$,$\sqrt{3}$),C(2$\sqrt{3}$,0),O(0,0),将这个平行四边形向左平移$\sqrt{3}$个单位长度,得到平行四边形A′B′C′O′,求平行四边形A′B′C′O′四个顶点的坐标.
如图,平行四边形ABCO四个顶点的坐标分别为A($\sqrt{3}$,$\sqrt{3}$),B(3$\sqrt{3}$,$\sqrt{3}$),C(2$\sqrt{3}$,0),O(0,0),将这个平行四边形向左平移$\sqrt{3}$个单位长度,得到平行四边形A′B′C′O′,求平行四边形A′B′C′O′四个顶点的坐标.