题目内容
10．
如图，在平面直角坐标系中，直线y=-x+6与x轴交于点B，与y轴交于点A，点C是线段AB的中点，求线段OC的长．
分析 求出A、B的坐标，根据直角三角形斜边上的中线等于斜边的一半解答．
解答 解：当x=0时，y=6；当y=0时，x=6，
则A（0，6），B（6，0），
在Rt△AOB中，AB=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$，
则OC=$\frac{1}{2}$AB=$\frac{1}{2}$×6$\sqrt{2}$=3$\sqrt{2}$．
点评 本题考查了勾股定理，利用平面直角坐标系的直角构造直角三角形是解题的关键．
练习册系列答案
相关题目
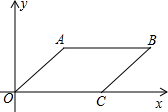如图，平行四边形ABCO四个顶点的坐标分别为A（$\sqrt{3}$，$\sqrt{3}$），B（3$\sqrt{3}$，$\sqrt{3}$），C（2$\sqrt{3}$，0），O（0，0），将这个平行四边形向左平移$\sqrt{3}$个单位长度，得到平行四边形A′B′C′O′，求平行四边形A′B′C′O′四个顶点的坐标．
15．下列运算正确的是（ ）
| A． | $\sqrt{25}$=±5 | B． | |-3|=3 | C． | $\root{3}{9}$=3 | D． | $\sqrt{{（-4）}^{2}}$=-4 |