题目内容
6.在△ABC中,BD,CE是高,G,F分别是BC,DE的中点,则∠EFG=90°.分析 作出图形,连接DG、EG、FG,根据直角三角形斜边上的中线等于斜边的一半可得DG=EG=$\frac{1}{2}$BC,再根据等腰三角形三线合一的性质可得FG⊥DE,最后根据垂直的定义解答.
解答  解:如图,连接DG、EG、FG,
解:如图,连接DG、EG、FG,
∵BD,CE是高,G是BC的中点,
∴DG=EG=$\frac{1}{2}$BC,
∵点F是DE的中点,
∴FG⊥DE,
∴∠EFG=90°.
故答案为:90°.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记各性质是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
14.如果$\frac{1}{{s}_{1}}=\frac{1}{{t}_{1}}+\frac{1}{{t}_{2}}$,$\frac{1}{{s}_{2}}=\frac{1}{{t}_{1}}-\frac{1}{{t}_{2}}$,则$\frac{{s}_{1}}{{s}_{2}}$=( )
| A. | $\frac{{t}_{1}+{t}_{2}}{{t}_{2}-{t}_{1}}$ | B. | $\frac{{t}_{2}-{t}_{1}}{{t}_{2}+{t}_{1}}$ | C. | $\frac{{t}_{1}-{t}_{2}}{{t}_{2}+{t}_{1}}$ | D. | $\frac{{t}_{1}+{t}_{2}}{{t}_{1}-{t}_{2}}$ |
15.下列运算正确的是( )
| A. | $\sqrt{25}$=±5 | B. | |-3|=3 | C. | $\root{3}{9}$=3 | D. | $\sqrt{{(-4)}^{2}}$=-4 |
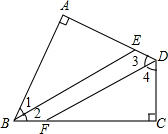 如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC(提示:四边形内角和等于360°).
如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC(提示:四边形内角和等于360°).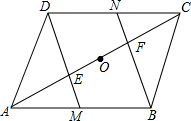 已知如图,O是?ABCD对角线AC的中点,E是AO的中点,F是OC的中点,联结DE并延长交AB于点M,联结BF并延长交CD于点N,求证:四边形DMBN是平行四边形.
已知如图,O是?ABCD对角线AC的中点,E是AO的中点,F是OC的中点,联结DE并延长交AB于点M,联结BF并延长交CD于点N,求证:四边形DMBN是平行四边形.