题目内容
4.设非零实数a,b满足:13a2+98a+1=0,b2+98b+13=0,求$\frac{ab+5a+1}{b}$的值.分析 a,$\frac{1}{b}$可以看成是方程13x2+98x+1=0的两根,利用根与系数关系即可解决问题
解答 解:∵13a2+98a+1=0,b2+98b+13=0,
∴a,$\frac{1}{b}$可以看成是方程13x2+98x+1=0的两根,
∴a+$\frac{1}{b}$=-$\frac{98}{13}$,$\frac{a}{b}$=$\frac{1}{13}$,
∴$\frac{ab+5a+1}{b}$=a+5•$\frac{a}{b}$+$\frac{1}{b}$=-$\frac{98}{13}$+$\frac{1}{13}$=-$\frac{97}{13}$.
点评 本题考查根与系数关系,解题的关键是记住x1+x2=$\frac{b}{a}$,x1x2=$\frac{c}{a}$,学会整体代入的思想解决问题,属于中考常考题型.

练习册系列答案
相关题目
13.已知一次函数y=kx+b(k≠0)不经过第一象限,则k、b的符号是( )
| A. | k<0,b<0 | B. | k<0,b>0 | C. | k>0,b<0 | D. | k<0,b≤0 |
 如图,点A、B、C、D在⊙O上,AC、BD相交于点P.则图中相似三角形有2对;若点C是$\widehat{BD}$的中点,则图中相似三角形有4对.
如图,点A、B、C、D在⊙O上,AC、BD相交于点P.则图中相似三角形有2对;若点C是$\widehat{BD}$的中点,则图中相似三角形有4对.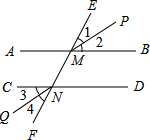 如图,下面四个条件中,请你以其中两个为已知条件,第三个作为结论,推出一个正确的命题.(只需写出一种情况)①AB∥CD;②∠1=∠4;③∠3=∠2;④MP∥NQ.
如图,下面四个条件中,请你以其中两个为已知条件,第三个作为结论,推出一个正确的命题.(只需写出一种情况)①AB∥CD;②∠1=∠4;③∠3=∠2;④MP∥NQ.